
 ,动圆
,动圆 过点
过点 且与圆
且与圆 相切,记动圆圆
相切,记动圆圆 的轨迹为
的轨迹为 .
. 的方程;
的方程; 为曲线
为曲线 上任意一点,证明直线
上任意一点,证明直线 与曲线
与曲线 恒有且只有一个公共点.
恒有且只有一个公共点. 写出一个类似的结论(皆不必证明).
写出一个类似的结论(皆不必证明). 圆心为
圆心为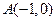 ,半径为
,半径为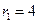 ,设动圆
,设动圆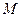 的圆心为
的圆心为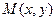
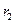 ,
,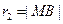 ,由
,由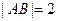 ,可知点
,可知点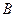 在圆
在圆 内,所以点
内,所以点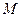 的轨迹是以
的轨迹是以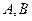 为焦点
为焦点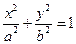
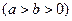 ,由
,由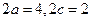 ,得
,得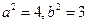 ,
, 的方程为
的方程为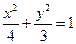 ………………………………4分
………………………………4分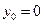 时,由
时,由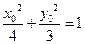 可得
可得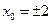
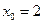 ,
,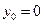 时,直线
时,直线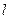 的方程为
的方程为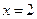 ,直线
,直线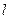 与曲线
与曲线 有且只有一个交点
有且只有一个交点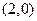
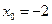 ,
,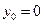 时,直线
时,直线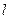 的方程为
的方程为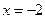 ,直线
,直线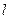 与曲线
与曲线 有且只有一个交点
有且只有一个交点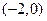
 时得
时得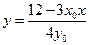 ,代入
,代入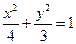 ,消去
,消去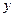 整理得:
整理得: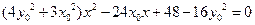 --------------------------------① …………6分
--------------------------------① …………6分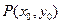 为曲线
为曲线 上一点,故
上一点,故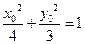 .即
.即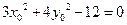
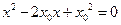
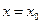 .将
.将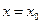 代入
代入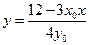 得
得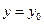 ,说明直线与曲线有且只有一个交点
,说明直线与曲线有且只有一个交点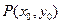 .
.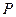 在何位置,直线
在何位置,直线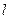 :
: 与曲线
与曲线 恒有且只有一个交点,交点即
恒有且只有一个交点,交点即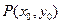 …………………………………………8分
…………………………………………8分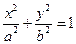
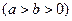 ,过其上任意一点
,过其上任意一点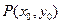 的切线方程为
的切线方程为 ;
; 中的类似的结论是:过双曲线
中的类似的结论是:过双曲线 上任意一点
上任意一点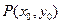 的切线方程为:
的切线方程为: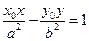 .…………………………………12分
.…………………………………12分

科目:高中数学 来源:不详 题型:解答题
 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为 .假设各次考试成绩合格与否均互不影响.
.假设各次考试成绩合格与否均互不影响. 率;
率; 弃所有的考试机会,记他参加考试的次数为
弃所有的考试机会,记他参加考试的次数为 ,求
,求 的数学期望E
的数学期望E .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(x+3)2+(y+2)2=2 | B.(x+3)2+(y+2)2= |
| C.(x+3)2+(y-2)2=2 | D.(x+3)2+(y-2)2= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com