练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．若一个扇形的弧长是3，半径是2，则该扇形的圆心角为（　　）
    A．$\frac{2}{3}$B．$\frac{3}{2}$C．6D．7

    分析 由已知利用弧长公式即可计算得解．

    解答 解：设扇形的弧长为l，圆心角大小为α（rad），半径为r，
    由已知可得：l=3，r=2，
    则由l=rα，可得：α=$\frac{l}{r}$=$\frac{3}{2}$．
    故选：B．

    点评 本题主要考查了弧长公式的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．已知直线l在平面α内，则“l⊥β”是“α⊥β”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

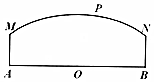    13．如图，两个工厂A，B相距8（单位：百米），O为AB的中点，曲线段MN上任意一点P到A，B的距离之和为10（单位：百米），且MA⊥AB，NB⊥AB．现计划在P处建一公寓，需考虑工厂A，B对它的噪音影响．工厂A对公寓的“噪音度”与距离AP成反比，比例系数为1；工厂B对公寓的“噪音度”与距离BP成反比，比例系数为k．“总噪音度”y是两个工厂对公寓的“噪音度”之和．经测算：当P在曲线段MN的中点时，“总噪音度”y恰好为1．
    （Ⅰ）设AP=x（单位：百米），求“总噪音度”y关于x的函数关系式，并求出该函数的定义域；
    （Ⅱ）当AP为何值时，“总噪音度”y最小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．（Ⅰ）求${（-\frac{7}{8}）^0}+{（\frac{1}{8}）^{-\;\;\frac{1}{3}}}+\root{4}{{{{（3-π）}^4}}}$的值；
    （Ⅱ）求${7^{{{log}_7}2}}+lg25+2lg2-ln\sqrt{e^3}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在四面体S-ABC中，$AB⊥BC，AB=BC=\sqrt{2}，SA=SC=2$，二面角S-AC-B的余弦值为$-\frac{{\sqrt{3}}}{3}$，则该四面体外接球的表面积是（　　）
    A．$8\sqrt{6}π$B．$\sqrt{6}π$C．24πD．6π

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．已知$α∈（\frac{5}{4}π\;，\;\frac{3}{2}π）$，且满足$tanα+\frac{1}{tanα}=8$，则sinαcosα=$\frac{1}{8}$；sinα-cosα=-$\frac{\sqrt{3}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．下列函数中，既是奇函数又在定义域内单调递增的是（　　）
    A．y=x3B．y=tanxC．$y={（\frac{1}{2}）^x}$D．y=lnx

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．设点A，B的坐标分别为（4，0），（-4，0），直线AP，BP相交于点P，且它们的斜率之积为实数m，关于点P的轨迹下列说法正确的是（　　）
    A．当m＜-1时，轨迹为焦点在x轴上的椭圆（除与x轴的两个交点）
    B．当-1＜m＜0时，轨迹为焦点在y轴上的椭圆（除与y轴的两个交点）
    C．当m＞0时，轨迹为焦点在x轴上的双曲线（除与x轴的两个交点）
    D．当0＜m＜1时，轨迹为焦点在y轴上的双曲线（除与y轴的两个交点）

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷（解析版） 题型：解答题

    已知数列的前项和为，且，数列满足

    （1）求，

    （2）求数列的前项和

    查看答案和解析>>

    同步练习册答案