
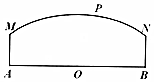
 ��ͼ����������A��B���8����λ�����ף���OΪAB���е㣬���߶�MN������һ��P��A��B�ľ���֮��Ϊ10����λ�����ף�����MA��AB��NB��AB���ּƻ���P����һ��Ԣ���迼�ǹ���A��B����������Ӱ�죮����A�Թ�Ԣ�ġ������ȡ������AP�ɷ��ȣ�����ϵ��Ϊ1������B�Թ�Ԣ�ġ������ȡ������BP�ɷ��ȣ�����ϵ��Ϊk�����������ȡ�y�����������Թ�Ԣ�ġ������ȡ�֮�ͣ������㣺��P�����߶�MN���е�ʱ�����������ȡ�yǡ��Ϊ1��
��ͼ����������A��B���8����λ�����ף���OΪAB���е㣬���߶�MN������һ��P��A��B�ľ���֮��Ϊ10����λ�����ף�����MA��AB��NB��AB���ּƻ���P����һ��Ԣ���迼�ǹ���A��B����������Ӱ�죮����A�Թ�Ԣ�ġ������ȡ������AP�ɷ��ȣ�����ϵ��Ϊ1������B�Թ�Ԣ�ġ������ȡ������BP�ɷ��ȣ�����ϵ��Ϊk�����������ȡ�y�����������Թ�Ԣ�ġ������ȡ�֮�ͣ������㣺��P�����߶�MN���е�ʱ�����������ȡ�yǡ��Ϊ1������ ��������AP��BP����ABΪx�ᣬ��O��Ϊ����ԭ�㣬������ͼ��ʾ��ֱ������ϵ��������߶�MN�ķ��̣��������������ȡ�y����x�ĺ�����ϵʽ��������ú����Ķ�����
����Ԫ�����û�������ʽ�����ɵó���APΪ��ֵʱ�����������ȡ�y��С��
��� 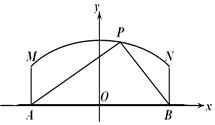 �⣺��������AP��BP������֪��AP=x��BP=10-x����1�֣�
�⣺��������AP��BP������֪��AP=x��BP=10-x����1�֣�
��y=$\frac{1}{x}$+$\frac{k}{10-x}$����3�֣�
��ABΪx�ᣬ��O��Ϊ����ԭ�㣬������ͼ��ʾ��ֱ������ϵ��
����Բ����ɵã����߶�MN�ķ��̣�$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1��-4��x��4������4�֣�
����֪��|MA|=$\frac{{b}^{2}}{a}$=$\frac{9}{5}$��|AN|=$\sqrt{64+\frac{81}{25}}$=$\frac{41}{5}$��
��$\frac{9}{5}��x��\frac{41}{5}$����5�֣�
����P�����߶�MN���е㼴AP=x=5ʱ��$\frac{1}{5}+\frac{k}{5}$=1��k=4��
������Ϊy=$\frac{1}{x}$+$\frac{4}{10-x}$��$\frac{9}{5}��x��\frac{41}{5}$������6�֣�
����y=$\frac{1}{x}$+$\frac{4}{10-x}$��$\frac{9}{5}��x��\frac{41}{5}$�����ɻ�Ϊy=$\frac{3x+10}{x��10-x��}$����7�֣�
��t=3x+10��t$��[\frac{77}{5}$��$\frac{183}{5}$]����8�֣�
��y=$\frac{9}{-��t+\frac{400}{t}��+50}$��$\frac{9}{10}$����10�֣�
���ҽ���t=$\frac{400}{t}$����t=20t$��[\frac{77}{5}$��$\frac{183}{5}$]��
��x=$\frac{10}{3}$ʱ�����������ȡ�y����СֵΪ$\frac{9}{10}$����12�֣�
���� ���⿼����Բ�Ķ��壬�����ı���ʽ����������ʽ��֪ʶ������ѧ���������������Ӧ����ѧ��������ת��Ϊͼ�����Լ��������Խ��������������������ν��˼������ѧӦ����ʶ��


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3}{10}$ | B�� | $\frac{2}{9}$ | C�� | $\frac{3}{5}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | t��1 | B�� | t��2$\sqrt{2}$-2 | C�� | t��2 | D�� | t��2$\sqrt{3}$-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.5Ԫ | B�� | 1Ԫ | C�� | 4.4Ԫ | D�� | 8Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $[-\frac{1}{2}��1]$ | B�� | $[-1��\frac{3}{2}]$ | C�� | $��-�ޣ�-1]��[\frac{3}{2}��+�ޣ�$ | D�� | [-2��1] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}}}{10}$ | B�� | $-\frac{{\sqrt{2}}}{10}$ | C�� | $\frac{{7\sqrt{2}}}{10}$ | D�� | $-\frac{{7\sqrt{2}}}{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{3}$ | B�� | $\frac{3}{2}$ | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com