练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．4支水笔与5支铅笔的价格之和不小于22元，6支水笔与3支铅笔的价格之和不大于24元，则1支水笔与1支铅笔的价格的差的最大值是（　　）
    A．0.5元B．1元C．4.4元D．8元

    分析 设1支水笔与1支铅笔的价格分别为x元、y元，根据条件列出不等式以及目标函数，利用简单线性规划即可求得结论

    解答 解：设1支水笔与1支铅笔的价格分别为x元、y元，则$\left\{\begin{array}{l}{4x+5y≥22}\\{6x+3y≤24}\\{x，y∈N}\end{array}\right.$，对应的区域如图
    设1支水笔与1支铅笔的价格的差z=x-y，即y=x-z，则直线经过A（3，2）时使得z最大为3-2=1，
    所以1支水笔与1支铅笔的价格的差的最大值是4；
    故选：B．

    点评 本题考查利用简单线性规划解决实际应用问题，需要根据题意列出约束条件以及目标函数；着重考查了二元一次不等式组表示的平面区域和简单的线性规划的应用等知识．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    18．下列函数中，为奇函数又在（0，+∞）上为减函数的是（　　）
    A．y=x-1B．y=sinxC．y=（$\frac{1}{2}$）xD．y=-|x|

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．“a＜2“是“方程x2+y2-2x+2y+a=0表示圆“的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．在△ABC中，角A，B，C所对的边分别为a，b，c，且bcosC+ccosB=$\sqrt{2}$acosC，则角C为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{π}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．一个三角形三边是连续的三个自然数，且最大角是最小角的2倍，则这个三角形的周长等于15．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

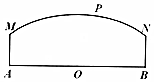    13．如图，两个工厂A，B相距8（单位：百米），O为AB的中点，曲线段MN上任意一点P到A，B的距离之和为10（单位：百米），且MA⊥AB，NB⊥AB．现计划在P处建一公寓，需考虑工厂A，B对它的噪音影响．工厂A对公寓的“噪音度”与距离AP成反比，比例系数为1；工厂B对公寓的“噪音度”与距离BP成反比，比例系数为k．“总噪音度”y是两个工厂对公寓的“噪音度”之和．经测算：当P在曲线段MN的中点时，“总噪音度”y恰好为1．
    （Ⅰ）设AP=x（单位：百米），求“总噪音度”y关于x的函数关系式，并求出该函数的定义域；
    （Ⅱ）当AP为何值时，“总噪音度”y最小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若函数$f（x）={log_{（2a-1）}}（{a^2}-2a+1）$的值为正数，则a的取值范围是（　　）
    A．（0，2）B．$（0，\frac{1}{2}）∪（1，2）$C．（-∞，0）∪（2，+∞）D．$（\frac{1}{2}，1）∪（2，+∞）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在四面体S-ABC中，$AB⊥BC，AB=BC=\sqrt{2}，SA=SC=2$，二面角S-AC-B的余弦值为$-\frac{{\sqrt{3}}}{3}$，则该四面体外接球的表面积是（　　）
    A．$8\sqrt{6}π$B．$\sqrt{6}π$C．24πD．6π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若f（x）=2cos（ωx+φ）+k，对任意实数t都有$f（\frac{π}{3}+t）=f（\frac{π}{3}-t）$成立，且$f（\frac{π}{3}）=-1$，则实数k的值等于（　　）
    A．-3或1B．1C．-1或3D．-3

    查看答案和解析>>

    同步练习册答案