
| A. | -3或1 | B. | 1 | C. | -1或3 | D. | -3 |
分析 通过有$f(\frac{π}{3}+t)=f(\frac{π}{3}-t)$成立,判断函数的对称轴,就是函数取得最值的x值,结合$f(\frac{π}{3})=-1$,即可求出k的值.
解答 解:因为f(x)=2cos(ωx+φ)+m,对任意实数t都有$f(\frac{π}{3}+t)=f(\frac{π}{3}-t)$成立,
所以函数的对称轴是x=$\frac{π}{3}$,就是函数取得最值,又$f(\frac{π}{3})=-1$,
所以-1=±2+k,所以k=1或-3.
故选:A.
点评 本题是基础题,考查三角函数的对称轴的应用,不求解析式,直接判断字母的值的方法,考查学生灵活解答问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | 0.5元 | B. | 1元 | C. | 4.4元 | D. | 8元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,1,2} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
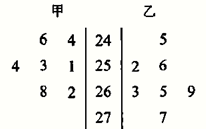 “双十一”网购狂欢,快递业务量猛增.甲、乙两位快递员11月12日到18日每天送件数量的茎叶图如图所示.
“双十一”网购狂欢,快递业务量猛增.甲、乙两位快递员11月12日到18日每天送件数量的茎叶图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com