
分析 (Ⅰ)函数f(x)=kx2+2x为奇函数,f(-x)=-f(x),即kx2-2x=-kx2-2x,即可求实数k的值;
(Ⅱ)g(x)=a2x-1,分类讨论,求g(x)在[-1,2]上的最小值.
解答 解:(Ⅰ)∵函数f(x)=kx2+2x为奇函数,
∴f(-x)=-f(x),即kx2-2x=-kx2-2x,
∴k=0;
(Ⅱ)g(x)=a2x-1,
0<a<1,函数g(x)在[-1,2]上单调递减,x=2时g(x)在[-1,2]上的最小值为a4-1;
a>1,函数g(x)在[-1,2]上单调递增,x=-1时g(x)在[-1,2]上的最小值为a-2-1.
点评 本题考查函数的奇偶性、最小值,考查分类讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | $(0,\frac{1}{2})∪(1,2)$ | C. | (-∞,0)∪(2,+∞) | D. | $(\frac{1}{2},1)∪(2,+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{6}π$ | B. | $\sqrt{6}π$ | C. | 24π | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=tanx | C. | $y={(\frac{1}{2})^x}$ | D. | y=lnx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
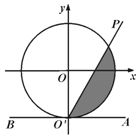 如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.
如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3或1 | B. | 1 | C. | -1或3 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com