
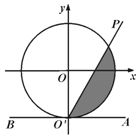
 ��ͼ����ƽ��ֱ������ϵxOy�У���λԲO��y�Ḻ���ύ�ڵ�O'������O'����x��ƽ�е�ֱ��AB������O'P��O'A���������ŵ�O'��ʱ�뷽����ת��O'B������ת�Ĺ����У��ǡ�AO'P=x��0��x���У���O'P���������ڵ�λԲO��������Ӱ���֣������ΪS��
��ͼ����ƽ��ֱ������ϵxOy�У���λԲO��y�Ḻ���ύ�ڵ�O'������O'����x��ƽ�е�ֱ��AB������O'P��O'A���������ŵ�O'��ʱ�뷽����ת��O'B������ת�Ĺ����У��ǡ�AO'P=x��0��x���У���O'P���������ڵ�λԲO��������Ӱ���֣������ΪS������ ��1��������$x=\frac{��}{2}$��O'P���������ڵ�λԲO��������Ӱ���֣������ΪSΪ�����λԲ��
��2���ٶ�����$x�ʣ�0��\frac{��}{2}��$������ͼ�οɵ�f��x��+f����-x���պ�Ϊ��λԲ������У�$0��\frac{��}{2}-x��\frac{��}{2}$⇒$f��\frac{��}{2}-x��+f��\frac{��}{2}+x��=��$��
��������ɵú���S=f��x���������������ж���
��� �⣺��1�������⣬ԲO�İ뾶Ϊ1�����$x=\frac{��}{2}$����ôS=$\frac{1}{2}��$�С�12=$\frac{��}{2}$��
��2���ٶ�����$x�ʣ�0��\frac{��}{2}��$������ͼ�οɵ�f��x��+f����-x���պ�Ϊ��λԲ������У���$0��\frac{��}{2}-x��\frac{��}{2}$⇒$f��\frac{��}{2}-x��+f��\frac{��}{2}+x��=��$���ʢ���ȷ��
��������ɵú���S=f��x�������������Զ�����x1��x2�ʣ�0���У�����x1��x2������$\frac{{f��{x_1}��-f��{x_2}��}}{{{x_1}-{x_2}}}��0$����
�ʴ�Ϊ����
���� ���⿼���˺�����������ʵ������Ľ�ϣ�ͨ������ͼ�εõ������ĶԳ��ԡ��������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
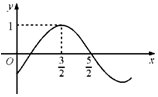
| A�� | $��=\frac{��}{2}����=-\frac{��}{4}$ | B�� | ��=$\frac{��}{2}����=\frac{��}{4}$ | C�� | $��=����=-\frac{��}{4}$ | D�� | $��=����=\frac{��}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {-1��0��1} | B�� | {0��1��2} | C�� | {0��1} | D�� | {1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {0} | B�� | {-1��0} | C�� | {1��2} | D�� | {-1��0��1��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2015-2016ѧ�����ʡ�����и�һ��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ�ѡ����
����ʽ �Ľ⼯�� �� ��
�Ľ⼯�� �� ��
A��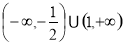 B��
B��
C��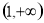 D��
D��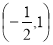
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com