

科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{6}π$ | B. | $\sqrt{6}π$ | C. | 24π | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=tanx | C. | $y={(\frac{1}{2})^x}$ | D. | y=lnx |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
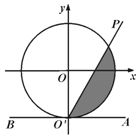 如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.
如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当m<-1时,轨迹为焦点在x轴上的椭圆(除与x轴的两个交点) | |
| B. | 当-1<m<0时,轨迹为焦点在y轴上的椭圆(除与y轴的两个交点) | |
| C. | 当m>0时,轨迹为焦点在x轴上的双曲线(除与x轴的两个交点) | |
| D. | 当0<m<1时,轨迹为焦点在y轴上的双曲线(除与y轴的两个交点) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3或1 | B. | 1 | C. | -1或3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:解答题
前不久商丘市因环境污染严重被环保部约谈后,商丘市近期加大环境治理力度,下表提供了商丘某企业节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程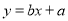 ;
;
(Ⅱ)已知该企业技改前100吨甲产品的生产能耗为90吨标准煤,试根据(Ⅰ)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)参考公式: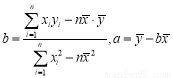
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com