
| A. | $8\sqrt{6}π$ | B. | $\sqrt{6}π$ | C. | 24π | D. | 6π |
分析 取AC中点D,连接SD,BD,由题意可得∠SDB为二面角S-AC-B,取等边△SAC的中心E,找出O点为四面体的外接球球心.
解答 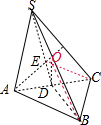 解:取AC中点D,连接SD,BD,
解:取AC中点D,连接SD,BD,
因为AB=BC=$\sqrt{2}$,所以BD⊥AC,
因为SA=SC=2,所以SD⊥AC,AC⊥平面SDB.
所以∠SDB为二面角S-AC-B.
在△ABC中,AB⊥BC,AB=BC=$\sqrt{2}$,
所以AC=2.
取等边△SAC的中心E,作EO⊥平面SAC,
过D作DO⊥平面ABC,O为外接球球心,
所以ED=$\frac{\sqrt{3}}{3}$,二面角S-AC-B的余弦值是-$\frac{\sqrt{3}}{3}$,所以cos∠EDO=$\frac{\sqrt{6}}{3}$,OD=$\frac{\sqrt{2}}{2}$,
所以BO=$\frac{\sqrt{6}}{2}$=OA=OS=OC
所以O点为四面体的外接球球心,
其半径为$\frac{\sqrt{6}}{2}$,表面积为6π.
故选:D.
点评 解决此类问题的关键是熟悉几何体的结构特征,利用已知条件求出线段长度,进而确定圆心的位置即可求出圆的半径.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.5元 | B. | 1元 | C. | 4.4元 | D. | 8元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $-\frac{{7\sqrt{2}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
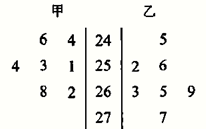 “双十一”网购狂欢,快递业务量猛增.甲、乙两位快递员11月12日到18日每天送件数量的茎叶图如图所示.
“双十一”网购狂欢,快递业务量猛增.甲、乙两位快递员11月12日到18日每天送件数量的茎叶图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com