
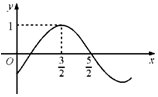
| A. | $ω=\frac{π}{2},φ=-\frac{π}{4}$ | B. | ω=$\frac{π}{2},φ=\frac{π}{4}$ | C. | $ω=π,φ=-\frac{π}{4}$ | D. | $ω=π,φ=\frac{π}{4}$ |
科目:高中数学 来源: 题型:选择题
| A. | (1,4) | B. | [1,4) | C. | (2,4) | D. | [2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 10 | C. | -10 | D. | -20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
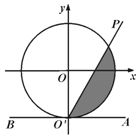 如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.
如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年湖北省仙桃市高一下学期期末考试数学试卷(解析版) 题型:选择题
有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为 ( )
A.2,4,6, 8 B.2,6,10,14
C.5,8,11,14 D.5,10,15,20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com