
| A. | $[-\frac{1}{2},1]$ | B. | $[-1,\frac{3}{2}]$ | C. | $(-∞,-1]∪[\frac{3}{2},+∞)$ | D. | [-2,1] |
分析 根据题意,由函数的奇偶性与单调性分析可得,$f({2^{2{x^2}-x-1}})≥f(-4)$?$f({2^{2{x^2}-x-1}})≥f(4)$?${2}^{2{x}^{2}-x-1}$≤4,结合指数函数的性质可得2x2-x-1≤2,解可得x的取值范围,即可得答案.
解答 解:根据题意,f(x)是偶函数,则$f({2^{2{x^2}-x-1}})≥f(-4)$?$f({2^{2{x^2}-x-1}})≥f(4)$,
且在区间(-∞,0]上递增,则函数在[0,+∞)上单调递减,则$f({2^{2{x^2}-x-1}})≥f(4)$?${2}^{2{x}^{2}-x-1}$≤4,
而${2}^{2{x}^{2}-x-1}$≤4?${2}^{2{x}^{2}-x-1}$≤22,即2x2-x-1≤2,
解可得-1≤x≤$\frac{3}{2}$,即x的取值范围是[-1,$\frac{3}{2}$],
故选:B.
点评 本题考查函数奇偶性与单调性的综合应用,涉及二次不等式的解法,关键是利用函数的奇偶性与单调性,将原问题转化为关于x的不等式求解问题.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a | ■ |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) | ■ | 0.08 |
| 第5组 | [90,100] | 2 | b |
| 合计 | ■ | ■ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
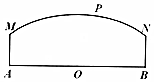 如图,两个工厂A,B相距8(单位:百米),O为AB的中点,曲线段MN上任意一点P到A,B的距离之和为10(单位:百米),且MA⊥AB,NB⊥AB.现计划在P处建一公寓,需考虑工厂A,B对它的噪音影响.工厂A对公寓的“噪音度”与距离AP成反比,比例系数为1;工厂B对公寓的“噪音度”与距离BP成反比,比例系数为k.“总噪音度”y是两个工厂对公寓的“噪音度”之和.经测算:当P在曲线段MN的中点时,“总噪音度”y恰好为1.
如图,两个工厂A,B相距8(单位:百米),O为AB的中点,曲线段MN上任意一点P到A,B的距离之和为10(单位:百米),且MA⊥AB,NB⊥AB.现计划在P处建一公寓,需考虑工厂A,B对它的噪音影响.工厂A对公寓的“噪音度”与距离AP成反比,比例系数为1;工厂B对公寓的“噪音度”与距离BP成反比,比例系数为k.“总噪音度”y是两个工厂对公寓的“噪音度”之和.经测算:当P在曲线段MN的中点时,“总噪音度”y恰好为1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2}\;,\;1)$ | B. | $[\frac{1}{2}\;,\;1)$ | C. | (1,+∞) | D. | $(\frac{1}{2},\;1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com