练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （理）已知命题α：2≤x，命题β：|x-m|≤1，且命题α是β的必要条件，求实数m的取值范围．
    分析：求出命题β的等价条件，利用命题α是β的必要条件，即可求出m的取值范围．
    解答：解：∵|x-m|≤1，
    ∴m-1≤x≤m+1，
    即β：m-1≤x≤m+1，
    ∵α是β的必要条件，
    ∴m-1≥2，
    即m≥3．
    点评：本题主要考查充分条件和必要条件的应用，利用绝对值不等式的解法求出等价条件是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （理）已知等差数列{an}中，a3=7，a1+a2+a3=12，令bn=anan+1，数列{
    1
    bn
    }    的前n项和为Tn．n∈N*．
    （1）求{an}的通项公式；
    （2）求证：Tn＜
    1
    3
    ；
    （3）通过对数列{Tn}的探究，写出“T1，Tm，Tn成等比数列”的一个真命题并说明理由（1＜m＜n，m，n∈N*）．
    说明：对于第（3）题，将根据对问题探究的完整性，给予不同的评分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•奉贤区二模）（理）已知函数f(x)=
    .
    sinxcosx
    -sinαcosα
    .
    ，g(x)=
    .
    cosxsinx
    sinβcosβ
    .
    ，α，β是参数，x∈R，α∈(-
    π
    2
    ，
    π
    2
    )    ，β∈(-
    π
    2
    ，
    π
    2
    )
    （1）若α=
    π
    4
    ，β=
    π
    4
    ，判别h（x）=f（x）+g（x）的奇偶性；
    若α=-
    π
    4
    ，β=
    π
    4
    ，判别h（x）=f2（x）+g2（x）的奇偶性；
    （2）若α=
    π
    3
    ，t（x）=f（x）g（x）是偶函数，求β；
    （3）请你仿照问题（1）（2）提一个问题（3），使得所提问题或是（1）的推广或是问题（2）的推广，问题（1）或（2）是问题（3）的特例．（不必证明命题）
    将根据写出真命题所体现的思维层次和对问题探究的完整性，给予不同的评分．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （06年江西卷理）已知圆M：（x＋cosq）2＋（y－sinq）2＝1，

    直线l：y＝kx，下面四个命题：

    (A)对任意实数k与q，直线l和圆M相切；

    (B)对任意实数k与q，直线l和圆M有公共点；

    (C)对任意实数q，必存在实数k，使得直线l与

    和圆M相切

    (D)对任意实数k，必存在实数q，使得直线l与

    和圆M相切

    其中真命题的代号是______________（写出所有真命题的代号）

    查看答案和解析>>

    科目：高中数学 来源：2011年上海市奉贤区高考数学三模试卷（文理合卷）（解析版） 题型：解答题

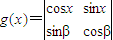    （理）已知函数，，α，β是参数，x∈R，，
    （1）若，判别h（x）=f（x）+g（x）的奇偶性；
    若，判别h（x）=f2（x）+g2（x）的奇偶性；
    （2）若，t（x）=f（x）g（x）是偶函数，求β；
    （3）请你仿照问题（1）（2）提一个问题（3），使得所提问题或是（1）的推广或是问题（2）的推广，问题（1）或（2）是问题（3）的特例．（不必证明命题）
    将根据写出真命题所体现的思维层次和对问题探究的完整性，给予不同的评分．

    查看答案和解析>>

    同步练习册答案