
分析 根据题意和一元一次不等式的解法列出不等式组,求出a、b的关系和符号,代入分式不等式化简后等价转化,由一元二次不等式的解法求出答案.
解答 解:由题意知,不等式ax-b>0的解集是(1,+∞),
则当且仅当a>0时,不等式ax-b>0的解集为$({\frac{b}{a}\;,\;+∞})$,
所以$\left\{\begin{array}{l}a>0\\ \frac{b}{a}=1\end{array}\right.$,即b=a>0,
所以不等式 $\frac{ax+b}{x-2}≤3a-b$可化为 $\frac{x+1}{x-2}≤2$,则$\frac{x+1}{x-2}-2≤0$,
即$\frac{5-x}{x-2}≤0$,即$\frac{x-5}{x-2}≥0$,等价于$\left\{\begin{array}{l}({x-2})({x-5})≥0\\ x-2≠0\end{array}\right.$,
解得x<2或x≥5,其解集为 (-∞,2)∪[5,+∞),
故答案为:(-∞,2)∪[5,+∞).
点评 本题考查分式不等式的解法及其转化,一元一次、一元二次不等式的解法,考查转化思想,化简、变形能力.


科目:高中数学 来源: 题型:解答题
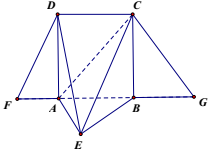 如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.
如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.
如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 0 | D. | 1-$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
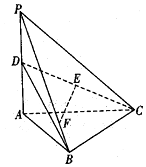 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com