
| A. | 命题“若x>1,则x2>1”的否命题 | |
| B. | 命题“若x=1,则x2+x-2=0”的否命题 | |
| C. | 命题“若x>y,则x>|y|”的逆命题 | |
| D. | 命题“若tanx=$\sqrt{3}$,则x=$\frac{π}{3}$”的逆否命题 |
分析 特殊值法判断A、B,根据不等式的性质判断C,判断原命题的正误判断其逆否命题的正误即可.
解答 解:对于A:命题“若x>1,则x2>1”的否命题是:
若x≤1,则x2≤1,是假命题,如,x=-5,x2=25;
对于B:命题“若x=1,则x2+x-2=0”的否命题是:
若x≠1,则x2+x-2≠0,是假命题,如:x=-2;
对于C:命题“若x>y,则x>|y|”的逆命题是:
若x>|y|,则x>y,是真命题;
对于D:命题“若tanx=$\sqrt{3}$,则x=$\frac{π}{3}$”是假命题,故其逆否命题是假命题;
故选:C.
点评 本题考查了四种命题的关系,考查三角函数的性质、不等式的性质,是一道基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 综合得分k的范围 | 产品级别 | 产品利润率 |
| k≥85 | 一级 | a |
| 75≤k<85 | 二级 | 5a2 |
| 70≤k<75 | 三级 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
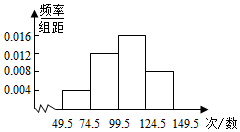 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右前三个小组的频率分别为 0.1,0.3,0.4,第一小组的频数为 5.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),已知图中从左到右前三个小组的频率分别为 0.1,0.3,0.4,第一小组的频数为 5.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=(0,+∞) | B. | M=N | C. | M∩N={0,1} | D. | M∩N=∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com