
【题目】下面(A)(B)(C)(D)为四个平面图形: 
(1)数出每个平面图形的交点数、边数、区域数,并将下表补充完整:
交点数 | 边数 | 区域数 | |
(A) | 4 | 5 | 2 |
(B) | 5 | 8 | |
(C) | 12 | 5 | |
(D) | 15 |
(2)观察表格,若记一个平面图形的交点数、边数、区域数分别为E、F、G,试猜想E、F、G之间的数量关系(不要求证明).
科目:高中数学 来源: 题型:
【题目】在每年的春节后,某市政府都会发动公务员参与到植树绿化活动中去.林业管理部门在植树前,为了保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两种树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.
(1)画出两组数据的茎叶图,并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为![]() ,将这10株树苗的高度依次输入,按程序框(如图)进行运算,问输出的S大小为多少?并说明S的统计学意义.
,将这10株树苗的高度依次输入,按程序框(如图)进行运算,问输出的S大小为多少?并说明S的统计学意义.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答题
(Ⅰ)某科考试中,从甲、乙两个班级各抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.设甲、乙两个班所抽取的10名同学成绩方差分别为 ![]() 、
、 ![]() ,比较
,比较 ![]() 、
、 ![]() 的大小(直接写结果,不必写过程);
的大小(直接写结果,不必写过程);
(Ⅱ)设集合 ![]() ,B={x|m+x2≤1,m<1},命题p:x∈A;命题q:x∈B,若p是q的必要条件,求实数m的取值范围.
,B={x|m+x2≤1,m<1},命题p:x∈A;命题q:x∈B,若p是q的必要条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保障高考的公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1 km内不能收到手机信号.检查员抽查青岛市一考点,在考点正西约![]() km有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以12 km/h的速度沿公路行驶,最长需要多少时间,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
km有一条北偏东60°方向的公路,在此处检查员用手机接通电话,以12 km/h的速度沿公路行驶,最长需要多少时间,检查员开始收不到信号,并至少持续多长时间该考点才算合格?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点是F1(﹣2,0),F2(2,0),且椭圆C经过点A(0, ![]() ).
).
(1)求椭圆C的标准方程;
(2)若过椭圆C的左焦点F1(﹣2,0)且斜率为1的直线l与椭圆C交于P、Q两点,求线段PQ的长(提示:|PQ|= ![]() |x1﹣x2|).
|x1﹣x2|).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了加强学生数学核心素养的培养,锻炼学生自主探究学习的能力,他们以函数![]() 为基本素材,研究该函数的相关性质,取得部分研究成果如下:
为基本素材,研究该函数的相关性质,取得部分研究成果如下:
①同学甲发现:函数![]() 的定义域为
的定义域为![]() ;
;
②同学乙发现:函数![]() 是偶函数;
是偶函数;
③同学丙发现:对于任意的![]() 都有
都有![]() ;
;
④同学丁发现:对于任意的![]() ,都有
,都有![]() ;
;
⑤同学戊发现:对于函数![]() 定义域中任意的两个不同实数
定义域中任意的两个不同实数![]() ,总满足
,总满足![]() .
.
其中所有正确研究成果的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子商务公司对10 000名网络购物者2017年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.
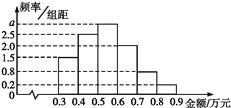
(1)直方图中的a=_____;
(2)在这些购物者中,消费金额在区间[0.5,0.9]内的购物者的人数为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义“三角恋写法”为“三个人之间写信,每人给另外两人之一写一封信,且任意两个人不会彼此给对方写信”,若五个人a,b,c,d,e中的每个人都恰给其余四人中的某一个人写了一封信,则不出现“三角恋写法”写法的写信情况的种数为( )
A.704
B.864
C.1004
D.1014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com