
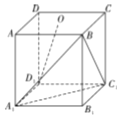
【题目】正四棱柱![]() 中,底面
中,底面![]() 的边长为1,
的边长为1,![]() 为正方形
为正方形![]() 的中心.
的中心.
(1)求证:![]() 平面
平面![]() ;
;
(2)若异面直线![]() 与
与![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求直线
,求直线![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)通过证明四边形一组对边平行且相等,得出四边形是平行四边形,从而得出另一组对边平行,得出线![]() 线,即可证出线
线,即可证出线![]() 面;
面;
(2)法一:通过已知异面直线![]() 与
与![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,可求出正方体的高
,可求出正方体的高![]() ,由(1)得出
,由(1)得出![]() 平面
平面![]() ,将直线
,将直线![]() 到平面
到平面![]() 的距离转化成点到面的距离,即点
的距离转化成点到面的距离,即点![]() 到平面
到平面![]() 的距离,再利用线面垂直的判定和性质,证出
的距离,再利用线面垂直的判定和性质,证出![]() 平面
平面![]() ,所以在直角三角形
,所以在直角三角形![]() 中,求出
中,求出![]() 的值,即可得出所求答案;
的值,即可得出所求答案;
法二:直线![]() 到平面
到平面![]() 的距离转化成点到面的距离,即点
的距离转化成点到面的距离,即点![]() 到平面
到平面![]() 的距离,再利用三棱锥等体积法求点到面的距离,即
的距离,再利用三棱锥等体积法求点到面的距离,即![]() ,化简便可求出结果.
,化简便可求出结果.
(1)连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,
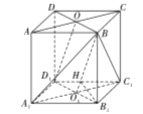
正四棱柱中,![]() ,且
,且![]() ,又因为点
,又因为点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,
所以![]() ,且
,且![]() ,
,
则四边形![]() 为平行四边形,故
为平行四边形,故![]() ,
,
又![]() 不在平面
不在平面![]() 内,
内,![]() 在平面
在平面![]() 内,
内,
故![]() 平面
平面![]() .
.
(2)由(1),![]() ,故异面直线
,故异面直线![]() 与
与![]() 所成的角等于
所成的角等于![]() ,
,
因为正四棱柱中,侧棱![]() 底面
底面![]() ,则
,则![]() ,
,
又![]() ,则
,则![]() 平面
平面![]() ,则
,则![]() .
.
因正方形![]() 的边长为1,则
的边长为1,则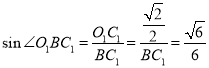 .
.
得![]() ,则
,则![]() .
.
因为![]() 平面
平面![]() ,则直线
,则直线![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
又![]() 为
为![]() 的中点,则点
的中点,则点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
在三角形![]() 内作
内作![]() ,因为
,因为![]() 平面
平面![]() ,
,
则平面![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
直角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
则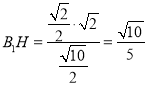 .
.
则直线![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
方法二(等体积法):
因为![]() 平面
平面![]() ,则直线
,则直线![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面的
到平面的![]() 的距离,
的距离,
又![]() 为
为![]() 的中点,则点
的中点,则点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离,
的距离,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() ,
,
![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
求得![]() .则直线
.则直线![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】若对任意的正整数![]() ,总存在正整数
,总存在正整数![]() ,使得数列
,使得数列![]() 的前
的前![]() 项和
项和![]() ,则称
,则称![]() 是“回归数列”.
是“回归数列”.
(1)①前![]() 项和为
项和为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
②通项公式为![]() 的数列
的数列![]() 是否是“回归数列”?并请说明理由;
是否是“回归数列”?并请说明理由;
(2)设![]() 是等差数列,首项
是等差数列,首项![]() ,公差
,公差![]() ,若
,若![]() 是“回归数列”,求
是“回归数列”,求![]() 的值;
的值;
(3)是否对任意的等差数列![]() ,总存在两个“回归数列”
,总存在两个“回归数列”![]() 和
和![]() ,使得
,使得![]() 成立,请给出你的结论,并说明理由.
成立,请给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
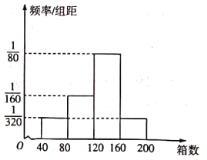
【题目】近几年一种新奇水果深受广大消费者的喜爱,一位农户发挥聪明才智,把这种露天种植的新奇水果搬到了大棚里,收到了很好的经济效益.根据资料显示,产出的新奇水果的箱数x(单位:十箱)与成本y(单位:千元)的关系如下:
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6.5 | 7 | 7.5 | 8 |
y与x可用回归方程![]() (其中
(其中![]() ,
,![]() 为常数)进行模拟.
为常数)进行模拟.
(1)若该农户产出的该新奇水果的价格为150元/箱,试预测该新奇水果100箱的利润是多少元.(利润=售价-成本)
(2)据统计,10月份的连续16天中该农户每天为甲地可配送的该新奇水果的箱数的频率分布直方图如图,用这16天的情况来估计相应的概率.一个运输户拟购置n辆小货车专门运输该农户为甲地配送的该新奇水果,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该新奇水果,满载发车,否则不发车.若发车,则每辆车每趟可获利500元,若未发车,则每辆车每天平均亏损200元试比较![]() 和
和![]() 时此项业务每天的利润平均值的大小.
时此项业务每天的利润平均值的大小.
参考数据与公式:设![]() ,则
,则
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
线性回归直线![]() 中,
中, ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一款手游,页面上有一系列的伪装,其中隐藏了4个宝藏.如果你在规定的时间内找到了这4个宝藏,将会弹出下一个页面,这个页面仍隐藏了2个宝藏,若能在规定的时间内找到这2个宝藏,那么闯关成功,否则闯关失败,结束游戏;如果你在规定的时间内找到了3个宝藏,仍会弹出下一个页面,但这个页面隐藏了4个宝藏,若能在规定的时间内找到这4个宝藏,那么闯关成功,否则闯关失败,结束游戏;其它情况下,不会弹出下一个页面,闯关失败,并结束游戏.
假定你找到任何一个宝藏的概率为![]() ,且能否找到其它宝藏相互独立..
,且能否找到其它宝藏相互独立..
(1)求闯关成功的概率;
(2)假定你付1个Q币游戏才能开始,能进入下一个页面就能获得2个Q币的奖励,闯关成功还能获得另外4个Q币的奖励,闯关失败没有额外的奖励.求一局游戏结束,收益的Q币个数X的数学期望(收益=收入-支出).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为![]() ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家污水处理厂有![]() 两个相同的装满污水的处理池,通过去掉污物处理污水,
两个相同的装满污水的处理池,通过去掉污物处理污水,![]() 池用传统工艺成本低,每小时去掉池中剩余污物的10%,
池用传统工艺成本低,每小时去掉池中剩余污物的10%,![]() 池用创新工艺成本高,每小时去掉池中剩余污物的19%.
池用创新工艺成本高,每小时去掉池中剩余污物的19%.
(1)![]() 池要用多长时间才能把污物的量减少一半;(精确到1小时)
池要用多长时间才能把污物的量减少一半;(精确到1小时)
(2)如果污物减少为原来的10%便符合环保规定,处理后的污水可以排入河流,若![]() 两池同时工作,问经过多少小时后把两池水混合便符合环保规定.(精确到1小时)
两池同时工作,问经过多少小时后把两池水混合便符合环保规定.(精确到1小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,右焦点F是抛物线
,右焦点F是抛物线![]() :
:![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上
上![]()
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 已知斜率为k的直线l交椭圆
已知斜率为k的直线l交椭圆![]() 于A,B两点,
于A,B两点,![]() ,直线AM与BM的斜率乘积为
,直线AM与BM的斜率乘积为![]() ,若在椭圆上存在点N,使
,若在椭圆上存在点N,使![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com