
【题目】近几年一种新奇水果深受广大消费者的喜爱,一位农户发挥聪明才智,把这种露天种植的新奇水果搬到了大棚里,收到了很好的经济效益.根据资料显示,产出的新奇水果的箱数x(单位:十箱)与成本y(单位:千元)的关系如下:
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6.5 | 7 | 7.5 | 8 |
y与x可用回归方程![]() (其中
(其中![]() ,
,![]() 为常数)进行模拟.
为常数)进行模拟.
(1)若该农户产出的该新奇水果的价格为150元/箱,试预测该新奇水果100箱的利润是多少元.(利润=售价-成本)
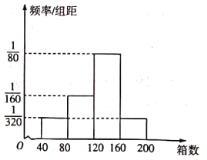
(2)据统计,10月份的连续16天中该农户每天为甲地可配送的该新奇水果的箱数的频率分布直方图如图,用这16天的情况来估计相应的概率.一个运输户拟购置n辆小货车专门运输该农户为甲地配送的该新奇水果,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40箱该新奇水果,满载发车,否则不发车.若发车,则每辆车每趟可获利500元,若未发车,则每辆车每天平均亏损200元试比较![]() 和
和![]() 时此项业务每天的利润平均值的大小.
时此项业务每天的利润平均值的大小.
参考数据与公式:设![]() ,则
,则
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
线性回归直线![]() 中,
中, ,
,![]() .
.
【答案】(1)6636(2)概率见解析,购置3辆小货车的利润平均值大于购置4辆小货车的利润平均值
【解析】
(1)根据题意,先求出![]() 关于
关于![]() 的线性回归方程,进而求得
的线性回归方程,进而求得![]() 关于
关于![]() 的线性回归方程,再将
的线性回归方程,再将![]() 代入回归方程,即可得答案;
代入回归方程,即可得答案;
(2)根据频率分布直方图,可得该农户每天可配送的该新奇水果的箱数的概率分情况,再设该运输户购3辆车和购4辆车时每天的利润分别为![]() ,
,![]() 元,写出两个随机变量的分布列,并求出期望进行大小比较,即可得答案.
元,写出两个随机变量的分布列,并求出期望进行大小比较,即可得答案.
(1)根据题意,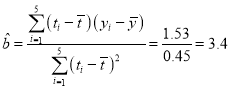 ,
,
所以![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
所以![]() 时,
时,![]() (千元),
(千元),
即该新奇水果100箱的成本为8364元,
故该新奇水果100箱的利润![]() .
.
(2)根据频率分布直方图,可知该农户每天可配送的该新奇水果的箱数的概率分布表为:
箱数 |
|
|
|
|
|
|
|
|
|
设该运输户购3辆车和购4辆车时每天的利润分别为![]() ,
,![]() 元.则
元.则![]() 的可能取值为1500,800,100,其分布列为
的可能取值为1500,800,100,其分布列为
| 1500 | 800 | 100 |
|
|
|
|
故![]() .
.
则![]() 的可能取值为2000,1300,600,
的可能取值为2000,1300,600,![]() ,其分布列为
,其分布列为
| 2000 | 1300 | 600 |
|
|
|
|
|
|
故![]() .
.
故![]() ,即购置3辆小货车的利润平均值大于购置4辆小货车的利润平均值.
,即购置3辆小货车的利润平均值大于购置4辆小货车的利润平均值.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,
,![]() 为任意实数.
为任意实数.
(1)求证:直线![]() 必与圆
必与圆![]() 相交;
相交;
(2)![]() 为何值时,直线
为何值时,直线![]() 被圆
被圆![]() 截得的弦长
截得的弦长![]() 最短?最短弦长是多少?
最短?最短弦长是多少?
(3)若直线![]() 被圆
被圆![]() 截得的弦
截得的弦![]() 的中点为点
的中点为点![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
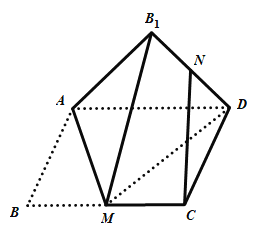
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 是我国古代著名数学经典
是我国古代著名数学经典![]() 其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小
其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小![]() 以锯锯之,深一寸,锯道长一尺
以锯锯之,深一寸,锯道长一尺![]() 问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺
问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺![]() 问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示
问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示![]() 阴影部分为镶嵌在墙体内的部分
阴影部分为镶嵌在墙体内的部分![]() 已知弦
已知弦![]() 尺,弓形高
尺,弓形高![]() 寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈
寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈![]() 尺
尺![]() 寸,
寸,![]() ,
,![]() )
)

A. 600立方寸 B. 610立方寸 C. 620立方寸 D. 633立方寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() ,点
,点![]() 是
是![]() 上的定点,
上的定点,![]() 、
、![]() 是
是![]() 上的两个动点,且线段
上的两个动点,且线段![]() 的中点
的中点![]() 在线段
在线段![]() 上.
上.
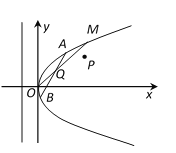
(1)抛物线![]() 的方程及
的方程及![]() 的值;
的值;
(2)当点![]() 、
、![]() 分别在第一、四象限时,求
分别在第一、四象限时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新中国成立70周年以来,党中央国务院高度重视改善人民生活,始终把提高人民生活水平作为一切工作的出发点和落脚点城乡居民收入大幅增长,居民生活发生了翻天覆地的变化.下面是1949年及2015年~2018年中国居民人均可支配收入(元)统计图.以下结论中不正确的是( )
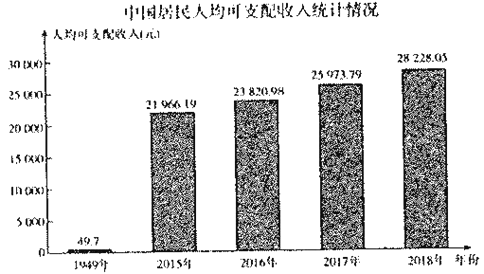
A.20l5年-2018年中国居民人均可支配收入与年份成正相关
B.2018年中居民人均可支配收入超过了1949年的500倍
C.2015年-2018年中国居民人均可支配收入平均超过了24000元
D.2015年-2018年中围居民人均可支配收入都超过了1949年的500倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】山东省2020年高考将实施新的高考改革方案.考生的高考总成绩将由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、历史、政治、地理6科中选择3门作为选考科目,语、数、外三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共8个等级。参照正态分布原则,确定各等级人数所占比例分别为
共8个等级。参照正态分布原则,确定各等级人数所占比例分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .等级考试科目成绩计入考生总成绩时,将
.等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到91-100、81-90、71-80,61-70、51-60、41-50、31-40、21-30八个分数区间,得到考生的等级成绩.
等级内的考生原始成绩,依照等比例转换法则,分别转换到91-100、81-90、71-80,61-70、51-60、41-50、31-40、21-30八个分数区间,得到考生的等级成绩.
举例说明.
某同学化学学科原始分为65分,该学科![]() 等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属
等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为61~70,那么该同学化学学科的转换分为:
等级的转换分区间为61~70,那么该同学化学学科的转换分为:
设该同学化学科的转换等级分为![]() ,
,![]() ,求得
,求得![]() .
.
四舍五入后该同学化学学科赋分成绩为67.
(1)某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布![]() .
.
(i)若小明同学在这次考试中物理原始分为84分,等级为![]() ,其所在原始分分布区间为82~93,求小明转换后的物理成绩;
,其所在原始分分布区间为82~93,求小明转换后的物理成绩;
(ii)求物理原始分在区间![]() 的人数;
的人数;
(2)按高考改革方案,若从全省考生中随机抽取4人,记![]() 表示这4人中等级成绩在区间
表示这4人中等级成绩在区间![]() 的人数,求
的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com