
| A. | {x|-3<x<0,或x>3} | B. | {x|x<-3,或0<x<3} | C. | {x|-3<x<0,或0<x<3} | D. | {x|x<-3,或x>3} |
分析 由x•f(x)<0对x>0或x<0进行讨论,把不等式x•f(x)<0转化为f(x)>0或f(x)<0的问题解决,根据f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,把函数值不等式转化为自变量不等式,求得结果.
解答 解:∵f(x)是R上的奇函数,且在(0,+∞)内是增函数,
∴在(-∞,0)内f(x)也是增函数,
又∵f(-3)=0,
∴f(3)=0
∴当x∈(-∞,-3)∪(0,3)时,f(x)<0;当x∈(-3,0)∪(3,+∞)时,f(x)>0;
∴x•f(x)<0的解集是(-3,0)∪(0,3)
故选C.
点评 考查函数的奇偶性和单调性解不等式,体现了分类讨论的思想方法,属中档题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
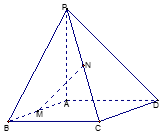 已知PA垂直于矩形ABCD所在平面,M,N分别是AB,PC的中点.
已知PA垂直于矩形ABCD所在平面,M,N分别是AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | [1,+∞) | C. | (2,+∞) | D. | [2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com