
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() .过
.过![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,过
,过![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,且
,且![]() 垂直
垂直![]() 于点
于点![]() .
.
(Ⅰ)证明:点![]() 在椭圆
在椭圆![]() 内部;
内部;
(Ⅱ)求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1)见解析(2)![]()
【解析】分析:
(Ⅰ)由![]() 可求得
可求得![]() ,从而椭圆标准方程,再由已知求出
,从而椭圆标准方程,再由已知求出![]() 点轨迹方程为
点轨迹方程为![]() ,而此圆在题设椭圆内部,因此可证P点在椭圆内部;
,而此圆在题设椭圆内部,因此可证P点在椭圆内部;
(Ⅱ)分类讨论,当![]() 斜率不存在时,可求出四边形ABCD的面积,同理当
斜率不存在时,可求出四边形ABCD的面积,同理当![]() 斜率不0时,
斜率不0时,
与刚才一样,当![]() 斜率存在且不为0时,设
斜率存在且不为0时,设![]() 方程为
方程为![]() ,这样就有
,这样就有![]() 方程为
方程为![]() ,设
,设![]() ,利用圆锥曲线中的弦长公式
,利用圆锥曲线中的弦长公式![]() 求得弦长
求得弦长![]() ,同理可得弦长
,同理可得弦长![]() ,于是可得面积
,于是可得面积![]() 为
为![]() 的函数,利用函数的知识可求得
的函数,利用函数的知识可求得![]() 的最小值,从而得出结论.
的最小值,从而得出结论.
详解:
(Ⅰ)由题意得![]() ,故
,故![]() ,所以椭圆方程为
,所以椭圆方程为![]() .
.
由于![]() 分别为过两焦点
分别为过两焦点![]() , 且垂直相交于点
, 且垂直相交于点![]() ,则
,则![]() 的轨迹为以
的轨迹为以![]() 为直径的圆,
为直径的圆,
即![]() 的轨迹方程为
的轨迹方程为![]() ,
,
又因为![]() ,所以点
,所以点![]() 在椭圆内部.
在椭圆内部.
(Ⅱ)①当![]() 斜率不存在时,直线
斜率不存在时,直线![]() 的方程为
的方程为![]() , 此时直线
, 此时直线![]() 的方程为
的方程为![]() ,
,
此时四边形![]() 的面积为
的面积为![]() .
.
同时当![]() 斜率为0时,此时
斜率为0时,此时![]() 的斜率不存在,易得
的斜率不存在,易得![]() .
.
②当![]() 斜率存在且不为0时,设直线
斜率存在且不为0时,设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,
,
设![]() ,联立
,联立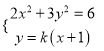 ,消去
,消去![]() 整理得
整理得![]() ,
,
所以![]() ,
,
所以![]() .
.
同理得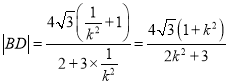
则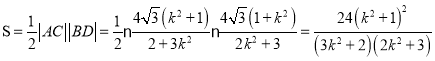
令![]() ,则
,则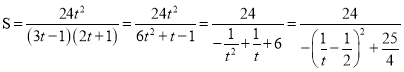
即当![]() ,即
,即![]() 时,
时, ![]()
综合上式①②可得,当![]() 时,
时, ![]() .
.
求最值的其它方法: 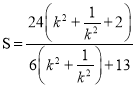 ,令
,令![]() ,得
,得![]() ,
,
因为![]() ,当
,当![]() 时,
时, ![]() ,且
,且![]() 是以
是以![]() 为自变量的增函数,所以
为自变量的增函数,所以![]() .
.
综上可知, ![]() . 即四边形
. 即四边形![]() 面积的最小值为
面积的最小值为![]() .
.
方法二:①当![]() 斜率为0,此时直线
斜率为0,此时直线![]() 轴,此时四边形
轴,此时四边形![]() 的面积为
的面积为![]() .
.
同时当![]() 斜率为0时,此时
斜率为0时,此时![]() 轴,易得
轴,易得![]() .
.
②当![]() 斜率存在且不为0时,设直线
斜率存在且不为0时,设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,
,
设![]() ,联立
,联立![]() ,消去
,消去![]() 整理得
整理得![]() ,
,
所以![]() ,
,
所以![]() .
.
同理得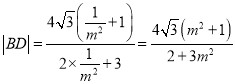
则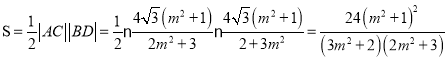
下同解法一.


科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(2)设函数![]() 的定义域为I,若
的定义域为I,若![]() ,且
,且![]() ,则称
,则称![]() 为函数
为函数![]() 的“壹点”,已知
的“壹点”,已知![]() 在区间
在区间![]() 上有4个不同的“壹点”,求实数
上有4个不同的“壹点”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求证二面角A1﹣BC1﹣B1的余弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络的飞速发展,人们的生活发生了很大变化,其中无现金支付是一个显著特征,某评估机构对无现金支付的人群进行网络问卷调查,并从参与调查的数万名受访者中随机选取了300人,把这300人分为三类,即使用支付宝用户、使用微信用户、使用银行卡用户,各类用户的人数如图所示,同时把这300人按年龄分为青年人组与中年人组,制成如图所示的列联表:
支付宝用户 | 非支付宝用户 | 合计 | |
中老年 | 90 | ||
青年 | 120 | ||
合计 | 300 |

(1) 完成列联表,并判断是否有99%的把握认为使用支付宝用户与年龄有关系?
(2)把频率作为概率,从所有无现金支付用户中(人数很多)随机抽取3人,用![]() 表示所选3人中使用支付宝用户的人数,求
表示所选3人中使用支付宝用户的人数,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 。
。
Ⅰ.求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
Ⅱ.当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
Ⅲ.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加![]() 元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费
元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费![]() 元,未租出的车每辆每月需要维护费
元,未租出的车每辆每月需要维护费![]() 元.
元.
(1)当每辆车的月租金定为![]() 元时,能租出多少辆车?
元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com