
【题目】已知函数![]() 图象在点
图象在点![]() (e为自然对数的底数)处的切线斜率为3.
(e为自然对数的底数)处的切线斜率为3.
(1)求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(1)a=1;(2)3.
【解析】试题分析:(1)先求出![]() 的导数f′(x)=a+lnx+1,根据已知条件f′(e)=3,再求出a+lne+1=3,可得a=1。
的导数f′(x)=a+lnx+1,根据已知条件f′(e)=3,再求出a+lne+1=3,可得a=1。
(2)根据已知条件建立一个不等式,再根据k<![]() 对任意x>1恒成立这个条件构造函数g(x)=
对任意x>1恒成立这个条件构造函数g(x)=![]() ,本题的目的就转化为求解g(x)的最小值,首先对g(x)求导,g′(x)=
,本题的目的就转化为求解g(x)的最小值,首先对g(x)求导,g′(x)=![]() ,无法直接判断g′(x)的符号,再构造一个函数h(x)=x﹣lnx﹣2,x>1,对其再进行求导,h′(x)=1﹣
,无法直接判断g′(x)的符号,再构造一个函数h(x)=x﹣lnx﹣2,x>1,对其再进行求导,h′(x)=1﹣![]() =
=![]() >0,显然h(x)在(1,+∞)单调递增,经计算确定h(x)在(3,4)内存在实根x0,所以当x∈(1,x0)时,h(x)<0,即g′(x)<0;当x∈(x0,+∞)时,h(x)>0,即g′(x)>0,所以g(x)min=g(x0)=
>0,显然h(x)在(1,+∞)单调递增,经计算确定h(x)在(3,4)内存在实根x0,所以当x∈(1,x0)时,h(x)<0,即g′(x)<0;当x∈(x0,+∞)时,h(x)>0,即g′(x)>0,所以g(x)min=g(x0)=![]() =
=![]() ∈(3,4),可得解.
∈(3,4),可得解.
试题解析:(1)由已知得f′(x)=a+lnx+1,故f′(e)=3,∴a+lne+1=3,
∴a=1
(2)由(1)知,f(x)=x+xlnx
等价于k<![]() 对任意x>1恒成立
对任意x>1恒成立
令g(x)=![]() ,则g′(x)=
,则g′(x)=![]()
令h(x)=x﹣lnx﹣2,x>1,
则h′(x)=1﹣![]() =
=![]() >0
>0
∴h(x)在(1,+∞)上单调增加,
∵h(3)=1﹣ln3<0,h(4)=2﹣2ln2>0,
∴h(x)在(1,+∞)上在唯一实数根x0,满足x0∈(3,4),且h(x0)=0
当x∈(1,x0)时,h(x)<0,∴g′(x)<0;当x∈(x0,+∞)时,h(x)>0,∴g′(x)>0,
∴g(x)=![]() 在(1,x0)上单调递减,在(x0,+∞)上单调递增
在(1,x0)上单调递减,在(x0,+∞)上单调递增
∴g(x)min=g(x0)=![]() =
=![]() ∈(3,4),
∈(3,4),
∴k<g(x)min=x0∈(3,4),
∴整数k的最大值为3.
点晴:本题主要考查函数在某点的切线的斜率,及不等式恒成立求参数问题.要求在某点的切线,求导得斜率,用点斜式表示切线方程即可;要证明不等式恒成立问题可变量分离转化为构造新函数求其值最值即可.这类问题的通解方法就是:划归与转化之后,就可以假设相对应的函数,然后利用导数研究这个函数的单调性、极值和最值,图像与性质,进而求解得结果.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】从1,3,5,7,9这五个数中,每次取出两个不同的数分别记为a,b,共可得到lga﹣lgb的不同值的个数是( )
A.9
B.10
C.18
D.20
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x),当x,y∈R时,恒有f(x+y)=f(x)+f(y).当x>0时,f(x)>0
(1)求证:f(x)是奇函数;
(2)若 ![]() ,试求f(x)在区间[﹣2,6]上的最值;
,试求f(x)在区间[﹣2,6]上的最值;
(3)是否存在m,使f(2( ![]() )2﹣4)+f(4m﹣2(
)2﹣4)+f(4m﹣2( ![]() ))>0对任意x∈[1,2]恒成立?若存在,求出实数m的取值范围;若不存在,说明理由.
))>0对任意x∈[1,2]恒成立?若存在,求出实数m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1.
(1)求函数f(x)的定义域;
(2)若函数f(x)的最小值为﹣4,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查 结果如下表所示:
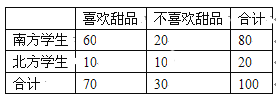
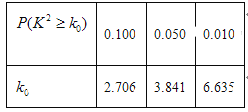
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
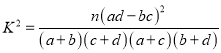 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且2csinBcosA﹣bsinC=0.
(1)求角A;
(2)若△ABC的面积为 ![]() ,b+c=5,求a.
,b+c=5,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2为椭圆C: ![]() =1(a>b>0)的左右焦点,O是坐标原点,过F2作垂直于x轴的直线MF2交椭圆于M,设|MF2|=d.
=1(a>b>0)的左右焦点,O是坐标原点,过F2作垂直于x轴的直线MF2交椭圆于M,设|MF2|=d.
(1)证明:b2=ad;
(2)若M的坐标为( ![]() ,1),求椭圆C的方程.
,1),求椭圆C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com