
已知函数
 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3),(1)求实数
的图像经过点(1,3),(1)求实数 的值;(2)求函数
的值;(2)求函数 的值域.
的值域.
(1) ; (2)函数
; (2)函数 的值域为
的值域为
解析试题分析:(1)由奇函数的定义可知 ,结合解析式可求
,结合解析式可求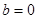 ,又由函数
,又由函数 的图像经过点(1,3),代入解析式可求得得
的图像经过点(1,3),代入解析式可求得得 ;(2)由(1)知
;(2)由(1)知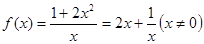 ,从而可由分类讨论的思想,分
,从而可由分类讨论的思想,分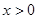 和
和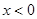 两种情况对函数的值域进行讨论,利用基本不等式可得函数
两种情况对函数的值域进行讨论,利用基本不等式可得函数 的值域为
的值域为 .本题注意分类讨论的思想方法的应用,易错点是基本不等式运用时的条件容易忽略.
.本题注意分类讨论的思想方法的应用,易错点是基本不等式运用时的条件容易忽略.
试题解析:(1) 函数
函数 是奇函数,则
是奇函数,则
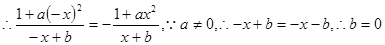 (3分)
(3分)
又函数 的图像经过点(1,3),
的图像经过点(1,3),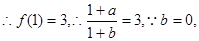
∴a=2 (6分)
(2)由(1)知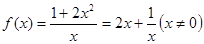 (7分)
(7分)
当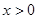 时,
时,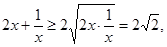 当且仅当
当且仅当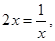
即 时取等号 (10分)
时取等号 (10分)
当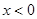 时,
时,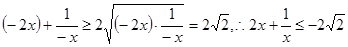
当且仅当 即
即 时取等号 (11分)
时取等号 (11分)
综上可知函数 的值域为
的值域为 (12分)
(12分)
考点:1.函数解析式的求法;2.函数的值域的求法;3.基本不等式的应用


科目:高中数学 来源: 题型:解答题
新晨投资公司拟投资开发某项新产品,市场评估能获得 万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金
万元的投资收益.现公司准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益 (单位:万元)的增加而增加,且奖金不低于
(单位:万元)的增加而增加,且奖金不低于 万元,同时不超过投资收益的
万元,同时不超过投资收益的 .
.
(1)设奖励方案的函数模型为 ,试用数学语言表述公司对奖励方案的函数模型
,试用数学语言表述公司对奖励方案的函数模型 的基本要求.
的基本要求.
(2)下面是公司预设的两个奖励方案的函数模型:
① ; ②
; ②
试分别分析这两个函数模型是否符合公司要求.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com