
若(x2-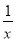 )n的展开式中含x的项为第6项,设(1-3x)n=a0+a1x+a2x2+…+anxn,则a1+a2+…+an的值为________.
)n的展开式中含x的项为第6项,设(1-3x)n=a0+a1x+a2x2+…+anxn,则a1+a2+…+an的值为________.
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:选择题
在高三的一个班中,有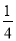 的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,
的学生数学成绩优秀,若从班中随机找出5名学生,那么数学成绩优秀的学生数ξ~B(5,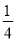 ),则P(ξ=k)取最大值的k值为( )
),则P(ξ=k)取最大值的k值为( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-4随机事件的概率(解析版) 题型:解答题
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
①假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
②若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-4随机事件的概率(解析版) 题型:选择题
5张卡片上分别写有数字1,2,3,4,5,从这5张卡片中随机抽取2张,则取出2张卡片上数字之和为偶数的概率为( )
A. B.
B.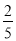 C.
C.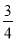 D.
D.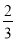
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:填空题
(2x+ )n的展开式中各项系数之和为729,则该展开式中x2的系数为________.
)n的展开式中各项系数之和为729,则该展开式中x2的系数为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:选择题
(2-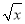 )8展开式中不含x4项的系数的和为( )
)8展开式中不含x4项的系数的和为( )
A.-1 B.0 C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:解答题
某区有7条南北向街道,5条东西向街道(如图).
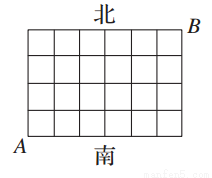
(1)图中共有多少个矩形?
(2)从A点走向B点最短的走法有多少种?
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:解答题
设数列{an}的各项均为正数.若对任意的n∈N*,存在k∈N*,使得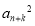 =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com