
设数列{an}的各项均为正数.若对任意的n∈N*,存在k∈N*,使得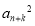 =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
(1)a2n=a2qn-1=(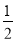 )n-4.
)n-4.
(2)见解析
【解析】【解析】
(1)由题意得a2,a4,a6,a8,…成等比数列,且公比q=(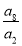 )
)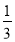 =
=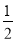 ,
,
所以a2n=(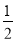 )n-4.
)n-4.
(2)由数列{an}是“J4型”数列,得
a1,a5,a9,a13,a17,a21,…成等比数列,设公比为t.
由数列{an}是“J3型”数列,得
a1,a4,a7,a10,a13,…成等比数列,设公比为α1;
a2,a5,a8,a11,a14,…成等比数列,设公比为α2;
a3,a6,a9,a12,a15,…成等比数列,设公比为α3.
则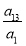 =α14=t3,
=α14=t3,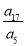 =α24=t3,
=α24=t3,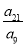 =α34=t3.
=α34=t3.
所以α1=α2=α3,不妨记α=α1=α2=α3,且t=α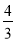 .
.
于是a3k-2=a1αk-1=a1(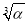 )(3k-2)-1,
)(3k-2)-1,
a3k-1=a5αk-2=a1tαk-2=a1αk-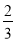 =a1(
=a1(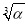 )(3k-1)-1,
)(3k-1)-1,
a3k=a9αk-3=a1t2αk-3=a1αk-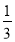 =a1(
=a1(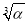 )3k-1,
)3k-1,
所以an=a1(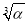 )n-1,故{an}为等比数列.
)n-1,故{an}为等比数列.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:填空题
若(x2-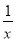 )n的展开式中含x的项为第6项,设(1-3x)n=a0+a1x+a2x2+…+anxn,则a1+a2+…+an的值为________.
)n的展开式中含x的项为第6项,设(1-3x)n=a0+a1x+a2x2+…+anxn,则a1+a2+…+an的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:填空题
某县从10名大学毕业的选调生中选3个人担任镇长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数为( )
A.85 B.56 C.49 D.28
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:选择题
已知集合A={y|y=(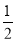 )x2+1,x∈R},则满足A∩B=B的集合B可以是( )
)x2+1,x∈R},则满足A∩B=B的集合B可以是( )
A.{0,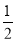 } B.{x|-1≤x≤1}
} B.{x|-1≤x≤1}
C.{x|0<x<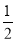 } D.{x|x>0}
} D.{x|x>0}
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练2(解析版) 题型:填空题
若对任意的x∈D,均有f1(x)≤f(x)≤f2(x)成立,则称函数f(x)为函数f1(x)到函数f2(x)在区间D上的“折中函数”.已知函数f(x)=(k-1)x-1,g(x)=0,h(x)=(x+1)ln x,且f(x)是g(x)到h(x)在区间[1,2e]上的“折中函数”,则实数k的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:填空题
我们把形如y=f(x)φ(x)的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得ln y=φ(x)lnf(x),两边求导得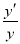 =φ′(x)·ln f(x)+φ(x)·
=φ′(x)·ln f(x)+φ(x)·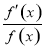 ,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·
,于是y′=f(x)φ(x)[φ′(x)·ln f(x)+φ(x)·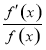 ].运用此方法可以探求得y=x
].运用此方法可以探求得y=x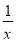 的单调递增区间是________.
的单调递增区间是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理配套特训:10-9离散型随机变量均值方差和正态分布(解析版) 题型:解答题
某示范性高中的校长推荐甲、乙、丙三名学生参加某大学自主招生考核测试,在本次考核中只有合格和优秀两个等级.若考核为合格,授予10分降分资格;考核为优秀, 授予20分降分资格.假设甲、乙、丙考核为优秀的概率分别为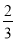 、
、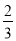 、
、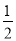 ,他们考核所得的等级相互独立.
,他们考核所得的等级相互独立.
(1)求在这次考核中,甲、乙、丙三名学生至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名学生所得降分之和为随机变量ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:7-1空间几何体结构及三视图和直观图(解析版) 题型:填空题
如图,一个封闭的三棱柱容器中盛有水,且侧棱长AA1=8.若侧面AA1B1B水平放置时,液面恰好经过AC,BC,A1C1,B1C1的中点. 当底面ABC水平放置时,液面高度为________.
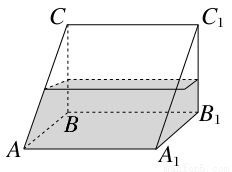
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:3-1任意角弧度制及任意角的三角函数(解析版) 题型:解答题
已知角α终边经过点P(x,-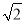 )(x≠0),且cosα=
)(x≠0),且cosα=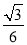 x,求sinα、tanα的值.
x,求sinα、tanα的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com