
若对任意的x∈D,均有f1(x)≤f(x)≤f2(x)成立,则称函数f(x)为函数f1(x)到函数f2(x)在区间D上的“折中函数”.已知函数f(x)=(k-1)x-1,g(x)=0,h(x)=(x+1)ln x,且f(x)是g(x)到h(x)在区间[1,2e]上的“折中函数”,则实数k的取值范围为________.
{2}
【解析】法一:依题意可知当x∈[1,2e]时,恒有0≤(k-1)x-1≤(x+1)ln x成立.
当x∈[1,2e]时,由(k-1)x-1≥0恒成立,可知k≥1+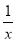 恒成立,又x∈[1,2e]时,
恒成立,又x∈[1,2e]时,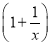 max=2,此时x=1,从而k≥2.
max=2,此时x=1,从而k≥2.
当x∈[1,2e]时,由(k-1)x-1≤(x+1)ln x恒成立,可知k≤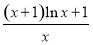 +1恒成立,记
+1恒成立,记
m(x)=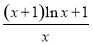 =
=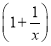 ln x+
ln x+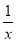 ,
,
其中x∈[1,2e].从而m′(x)=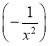 ln x+
ln x+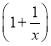
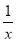 -
-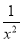 =
=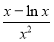 ,易知当x∈[1,2e]时,x>ln x(可以建立函数再次利用导数证明,)所以当x∈[1,2e]时,m′(x)>0,所以m(x)在x∈[1,2e]上是单调递增函数,所以k≤m(x)min+1=m(1)+1=2.
,易知当x∈[1,2e]时,x>ln x(可以建立函数再次利用导数证明,)所以当x∈[1,2e]时,m′(x)>0,所以m(x)在x∈[1,2e]上是单调递增函数,所以k≤m(x)min+1=m(1)+1=2.
综上所述可知k=2,所以实数k的取值范围为{2}.
法2:由于本题的特殊性,可看出g(1)=0,h(1)=0,由题知g(1)≤f(1)≤h(1),显然f(1)=0,即k=2.h′(x)=1+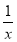 +ln x.在[1,2e]上,h′(x)>1=f′(x),故k=2.
+ln x.在[1,2e]上,h′(x)>1=f′(x),故k=2.


科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-4随机事件的概率(解析版) 题型:选择题
5张卡片上分别写有数字1,2,3,4,5,从这5张卡片中随机抽取2张,则取出2张卡片上数字之和为偶数的概率为( )
A. B.
B.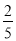 C.
C.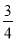 D.
D.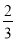
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-1分类加法与分步乘法计数原理(解析版) 题型:填空题
如果把个位数是1,且恰有3个数字相同的四位数叫作“好数”,那么在由1,2,3,4四个数字组成的有重复数字的四位数中,“好数”共有________个.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:填空题
设集合A={x|x= ,k∈N},B={x|0≤x≤6,x∈Q},则A∩B=________.
,k∈N},B={x|0≤x≤6,x∈Q},则A∩B=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练2(解析版) 题型:解答题
如图,两个圆形飞轮通过皮带传动,大飞轮O1的半径为2r(r为常数),小飞轮O2的半径为r,O1O2=4r.在大飞轮的边缘上有两个点A,B,满足∠BO1A=,在小飞轮的边缘上有点C.设大飞轮逆时针旋转,传动开始时,点B,C在水平直线O1O2上.
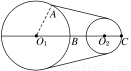
(1)求点A到达最高点时A,C间的距离;
(2)求点B,C在传动过程中高度差的最大值.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:解答题
设数列{an}的各项均为正数.若对任意的n∈N*,存在k∈N*,使得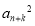 =an·an+2k成立,则称数列{an}为“Jk型”数列.
=an·an+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:填空题
已知两个非零向量a与b,定义|a×b|=|a|·|b|sin θ,其中θ为a与b的夹角.若a=(-3,4),b=(0,2),则|a×b|的值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:7-1空间几何体结构及三视图和直观图(解析版) 题型:选择题
一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( )

A.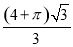 B.
B.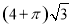
C.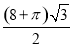 D.
D.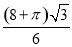
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:3-2同角三角函数基本关系式与诱导公式(解析版) 题型:选择题
已知2sinαtanα=3,则cosα的值是( )
A.-7 B.- C.
C.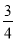 D.
D.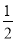
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com