已知集合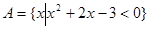
，
.
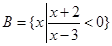（1）在区间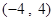
上任取一个实数
，求“
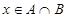”的概率；
（2）设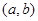
为有序实数对（如有序实数对（2,3）与（3,2）不一样），其中
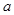是从集合
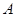中任取的一个整数，
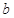是从集合
中任取的一个整数，求“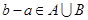
”的概率
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：解答题
设集合Sn={1，2，3，，n），若X是Sn的子集，把X中所有元素的和称为X的“容量”（规定空集的容量为0），若X的容量为奇（偶）数，则称X为Sn的奇（偶）子集．
（I）写出S4的所有奇子集；
（Ⅱ）求证：Sn的奇子集与偶子集个数相等；
（Ⅲ）求证：当n≥3时，Sn的所有奇子集的容量之和等于所有偶子集的容量之和．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（2013•重庆）对正整数n，记In={1，2，3…，n}，Pn={
|m∈In，k∈In}．
（1）求集合P7中元素的个数；
（2）若Pn的子集A中任意两个元素之和不是整数的平方，则称A为“稀疏集”．求n的最大值，使Pn能分成两个不相交的稀疏集的并．
查看答案和解析>>
科目：高中数学 来源： 题型：填空题
定义集合M、N的新运算如下：MxN＝{x|x∈M或x∈N，但x∉M∩N}，若集合M＝{0,2,4,6,8,10}，N＝{0,3,6,9,12,15}，则(MxN)xM等于________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.（2）
. 
，
，
.（2）由于
”的概率为
，这是一个几何概型，则概率
，且
，所以，基本事件共12个：
，
，
，
，
，
，
，
，
，
，
，
9分
为“
. 12分
,集合
,
,则
= .
.
求a的值;
,求a的值;
，
，则
（ ）.
，集合
，
，则
（ ）
,集合
,则
（ ）
