
设集合Sn={1,2,3,,n),若X是Sn的子集,把X中所有元素的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为Sn的奇(偶)子集.
(I)写出S4的所有奇子集;
(Ⅱ)求证:Sn的奇子集与偶子集个数相等;
(Ⅲ)求证:当n≥3时,Sn的所有奇子集的容量之和等于所有偶子集的容量之和.
(I)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析
解析试题分析:(I)根据奇子集的定义可直接得出,注意应按规律一一列出以防重写或漏写。(Ⅱ)取Sn的任意一个奇子集 可能含有1也可能不含1,当奇子集
可能含有1也可能不含1,当奇子集 含有1时,令
含有1时,令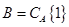 ,当奇子集
,当奇子集 不含1时,令
不含1时,令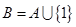 ,则
,则 为
为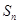 的偶子集,且
的偶子集,且 与
与 相对应,反之也成立。因为
相对应,反之也成立。因为 与
与 相对应即Sn的奇子集与偶子集个数相等。(Ⅲ)由(Ⅱ)知Sn的奇子集与偶子集个数相等,且Sn中每一个元素在奇子集与偶子集中出现的次数是相同的,所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
相对应即Sn的奇子集与偶子集个数相等。(Ⅲ)由(Ⅱ)知Sn的奇子集与偶子集个数相等,且Sn中每一个元素在奇子集与偶子集中出现的次数是相同的,所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
试题解析:(I)
(Ⅱ)对于Sn的每个奇子集 ,
,
当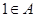 时,取
时,取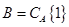 ;当
;当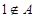 时,取
时,取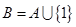 。
。
则 为
为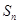 的偶子集。
的偶子集。
反之,若 为
为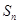 的偶子集,
的偶子集,
当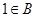 时,取
时,取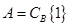 ;当
;当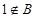 时,取
时,取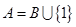 。
。
则 为
为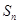 的奇子集。
的奇子集。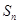 的奇子集与偶子集之间建立了一一对应的关系,所以
的奇子集与偶子集之间建立了一一对应的关系,所以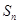 的奇子集和偶子集的个数相等。
的奇子集和偶子集的个数相等。
(Ⅲ)对于任意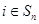 ,
,
当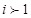 时,含
时,含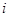 的
的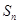 的子集共有
的子集共有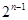 个。由(Ⅱ)可知,对每个数
个。由(Ⅱ)可知,对每个数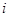
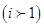 ,在奇子集与偶子集中,
,在奇子集与偶子集中,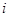 所占的个数是相等的;
所占的个数是相等的;
当 时,将(Ⅱ)中的1换成3即可。
时,将(Ⅱ)中的1换成3即可。
可知 在奇子集与偶子集中占的个数是相等。
在奇子集与偶子集中占的个数是相等。
综合(1)(2),每个元素都是在奇子集与偶子集中占的个数相等。
所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
考点:新概念问题。


科目:高中数学 来源: 题型:填空题
已知集合A、B,定义集合A与B的一种运算A⊕B,其结果如下表所示:
| A | {1,2,3,4} | {-1,1} | {-4,8} | {-1,0,1} |
| B | {2,3,6} | {-1,1} | {-4,-2,0,2} | {-2,-1,0,1} |
| A⊕B | {1,4,6} | ∅ | {-2,0,2,8} | {-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
集合A={x|-2≤x≤5},集合B={x|m+1≤x≤2m-1}.
(1) 若B A,求实数m的取值范围;
A,求实数m的取值范围;
(2) 当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知集合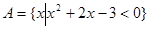 ,
,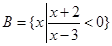 .
.
(1)在区间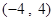 上任取一个实数
上任取一个实数 ,求“
,求“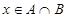 ”的概率;
”的概率;
(2)设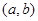 为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中
为有序实数对(如有序实数对(2,3)与(3,2)不一样),其中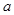 是从集合
是从集合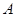 中任取的一个整数,
中任取的一个整数,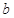 是从集合
是从集合 中任取的一个整数,求“
中任取的一个整数,求“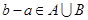 ”的概率
”的概率
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设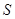 为复数集
为复数集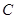 的非空子集.若对任意
的非空子集.若对任意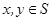 ,都有
,都有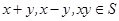 ,则称S为封闭集.下列命题:①集合S={a+bi|(
,则称S为封闭集.下列命题:①集合S={a+bi|(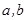 为整数,
为整数,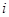 为虚数单位)}为封闭集;②若S为封闭集,则一定有
为虚数单位)}为封闭集;②若S为封闭集,则一定有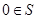 ;③封闭集一定是无限集;④若
;③封闭集一定是无限集;④若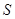 为封闭集,则满足
为封闭集,则满足 的任意集合
的任意集合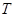 也是封闭集.其中真命题是 (写出所有真命题的序号).
也是封闭集.其中真命题是 (写出所有真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com