练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

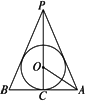
    如图，设球的半径为R，联系已知球半径、锥底半径和母线来表达外切于这个球的一切圆锥中全面积最小的圆锥的全面积．

    答案：
    解析：


    提示：

    球的半径是定值，但这个球的外切圆锥是相当自由的概念，锥高h＞2R，可大可小，锥底半径也随着锥高的变化而变化，如何选择一个恰当的自变量，可以互相兼顾，比较方便地勾勒出这些量，从而把外切圆锥的全面积表示为这个变量的函数，然后来求全面积这个目标函数的最小值，是一个很重要的问题．经过多方试探，这里给出一种选用∠OAC＝，来联系已知球半径、锥底半径和母线来表达全面积的方法，是比较理想的方法之一．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，在三棱锥S-ABC中，侧面SAB⊥底面ABC，且∠ASB=∠ABC=90°，AS=SB=2，AC=2
    		3
    ．

    （Ⅰ）求证SA⊥SC；
    （Ⅱ）在平面几何中，推导三角形内切圆的半径公式r=
    2S
    l
    （其中l是三角形的周长，S是三角形的面积），常用如下方法（如右图）：
    ①以内切圆的圆心O为顶点，将三角形ABC分割成三个小三角形：△OAB，△OAC，△OB精英家教网C．
    ②设△ABC三边长分别为a，b，c．由S△ABC=S△OBC+S△OAC+S△OAB，
    得S=
    1
    2
    ar+
    1
    2
    br+
    1
    2
    cr    =
    1
    2
    lr    ，则r=
    2S
    l
    ．
    类比上述方法，请给出四面体内切球半径的计算公式（不要求说明类比过程），并利用该公式求出三棱锥S-ABC内切球的半径．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

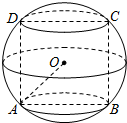    精英家教网如图，半径R=3的球O中有一内接圆柱，设圆柱的高为h，底面半径为r．
    （Ⅰ）当h=4时，求圆柱的体积与球的体积；
    （Ⅱ）当圆柱的轴截面ABCD的面积最大时，求h与r的值．

    查看答案和解析>>

    科目：高中数学 来源：高三数学教学与测试 题型：044

    已知球的半径为R，内切于顶点为P的圆锥(轴截面如图)．设∠＝θ．

    　　

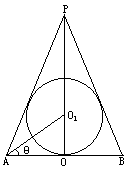
    (1)试用R，θ表示圆锥底面半径r，母线l和全面积S；

    (2)当θ为何值时，圆锥全面积取最小值？最小值是多少？

    查看答案和解析>>

    同步练习册答案