
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R).
(1)证明:不论m取什么实数时,直线l与圆恒交于两点;
(2)求直线l被圆C截得的线段的最短长度以及此时直线l的方程.
【答案】
(1)解:由m(2x+y﹣7)+(x+y﹣4)=0知直线l恒过定点,
又 ![]() ,
,
∴直线l恒过定点A(3,1),
且(3﹣1)2+(1﹣2)2=5<25A(3,1)必在圆内,
故直线l与圆恒有两交点
(2)解:∵圆心为C(1,2),定点为A(3,1)
∴ ![]()
由平面几何知识知,当直线l与AC垂直时所截线段最短,此时kl=2
∴l方程为:y﹣1=2(x﹣3)2x﹣y﹣5=0,此时 ![]()
∴最短弦长= ![]()
【解析】(1)把直线l的方程变形后,根据直线l恒过定点,得到关于x与y的二元一次方程组,求出方程组的解即为直线l恒过的定点坐标,然后利用两点间的距离公式求出此点到圆心的距离d,发现d小于圆的半径,得到此点在圆内,故直线l与圆恒交于两点;(2)由平面几何知识可知,当直线l与AC垂直时,所截取的线段最短,由圆心C和定点A的坐标求出直线AC的斜率,根据两直线垂直时斜率的乘积为﹣1,求出直线l的斜率,由A的坐标和求出的斜率写出直线l的方程,再由A与C的坐标,利用两点间的距离公式求出|AC|即为弦心距,根据圆的半径,弦心距及弦的一半构成的直角三角形,利用勾股定理即可求出此时的弦长.


科目:高中数学 来源: 题型:
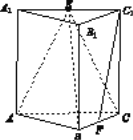
【题目】如图,在三棱柱ABC A1B1C1中,侧棱垂直于底面,AB⊥BC, ![]() ,
,
E,F分别是A1C1,BC的中点.
(Ⅰ)求证:C1F∥平面ABE;
(Ⅱ)求三棱锥E-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x﹣sinxcosx
(1)求f(x)的最小正周期;
(2)求函数f(x)的单调递增区间;
(3)求f(x)在区间 ![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意的x1∈[﹣1,2],存在x0∈[﹣1,2],使g(x1)=f(x0),则a的取值范围是( )
A.![]()
B.![]()
C.[3,+∞)
D.(0,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确命题的个数是( )
①若2b=a+c,则a,b,c成等差数列;
②“a,b,c成等比数列”的充要条件是“b2=ac”;
③若数列{an2}是等比数列,则数列{an}也是等比数列;
④若| ![]() |=|
|=| ![]() |,则
|,则 ![]() =
= ![]() .
.
A.3
B.2
C.1
D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数f(x)=loga(x+1),g(x)=2loga(2x+t)(t∈R),a>0,且a≠1.
(1)若1是关于x的方程f(x)﹣g(x)=0的一个解,求t的值;
(2)当0<a<1且t=﹣1时,解不等式f(x)≤g(x);
(3)若函数F(x)=af(x)+tx2﹣2t+1在区间(﹣1,2]上有零点,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
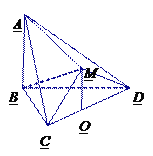
【题目】如图,在多面体![]() 中,△
中,△![]() 是等边三角形,△
是等边三角形,△![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
, ![]()
![]() 平面
平面![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
(1) 求证: ![]() ∥平面
∥平面![]() ;
;
(2)若![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}前n项和为Sn , 且Sn+an=2. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足b1=a1 , bn= ![]() ,n≥2 求证{
,n≥2 求证{ ![]() }为等比数列,并求数列{bn}的通项公式;
}为等比数列,并求数列{bn}的通项公式;
(Ⅲ)设cn= ![]() ,求数列{cn}的前n和Tn .
,求数列{cn}的前n和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com