
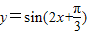 的图象向右平移
的图象向右平移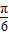 个单位长度后,再使平移后的图象纵坐标不变,横坐标伸长为原来的2倍,得到函数y=f(x)的图象,将方程xf(x)=1的所有正根按从小到大排成一个数列{an},在以下结论中:
个单位长度后,再使平移后的图象纵坐标不变,横坐标伸长为原来的2倍,得到函数y=f(x)的图象,将方程xf(x)=1的所有正根按从小到大排成一个数列{an},在以下结论中: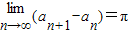 ;
;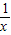 的图象在第一象限的交点横坐标,然后画出两函数的图形,结合图形可判定选项的真假.
的图象在第一象限的交点横坐标,然后画出两函数的图形,结合图形可判定选项的真假.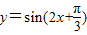 的图象向右平移
的图象向右平移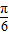 个单位长度后,
个单位长度后,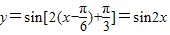 ,
,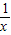 的图象在第一象限的交点横坐标
的图象在第一象限的交点横坐标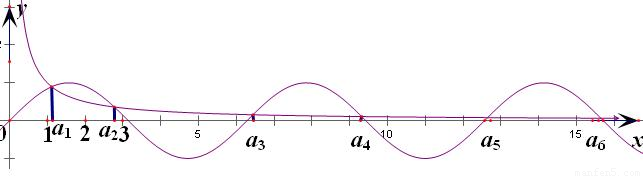
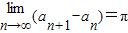 ,正确;
,正确;

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 )的最高点D的坐标为(
)的最高点D的坐标为(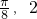 ),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(
),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(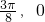 );
);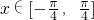 时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.
时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值. 个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.
个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东汕头四中高一上期末考试数学试卷(带解析) 题型:解答题
(本小题满分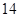 分)设函数
分)设函数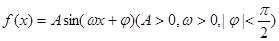 的最高点
的最高点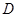 的坐标为(
的坐标为(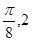 ),由最高点
),由最高点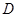 运动到相邻最低点时,函数图形与
运动到相邻最低点时,函数图形与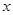 的交点的坐标为(
的交点的坐标为(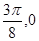 ).
).
(1)求函数 的解析式.
的解析式.
(2)当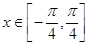 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时
的最大值和最小值以及分别取得最大值和最小值时
相应的自变量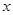 的值.
的值.
(3)将函数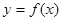 的图象向右平移
的图象向右平移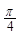 个单位,得到函数
个单位,得到函数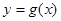 的图象,求函数
的图象,求函数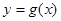 的单调减区间.
的单调减区间.
查看答案和解析>>
科目:高中数学 来源:2009-2010学年广东省东莞五校高一(下)期中数学试卷(解析版) 题型:解答题
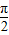 )的最高点D的坐标为(
)的最高点D的坐标为(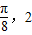 ),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(
),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(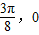 );
);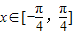 时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.
时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.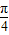 个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.
个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.查看答案和解析>>
科目:高中数学 来源:2015届广东汕头四中高一上期末考试数学试卷(解析版) 题型:解答题
(本小题满分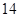 分)设函数
分)设函数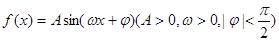 的最高点
的最高点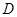 的坐标为(
的坐标为(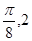 ),由最高点
),由最高点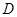 运动到相邻最低点时,函数图形与
运动到相邻最低点时,函数图形与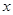 的交点的坐标为(
的交点的坐标为(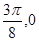 ).
).
(1)求函数 的解析式.
的解析式.
(2)当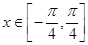 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时
的最大值和最小值以及分别取得最大值和最小值时
相应的自变量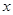 的值.
的值.
(3)将函数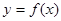 的图象向右平移
的图象向右平移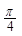 个单位,得到函数
个单位,得到函数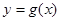 的图象,求函数
的图象,求函数
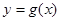 的单调减区间.
的单调减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com