Question

已知函数f(x)=

1

2

x2-(1+a)x+alnx，其中a＞0．
（Ⅰ） 求函数f（x）的极小值点；
（Ⅱ）若曲线y=f（x）在点A（m，f（m）），B（n，f（n））处的切线都与y轴垂直，问是否存在常数a，使函数y=f（x）在区间[m，n]上存在零点？如果存在，求a的值：如果不存在，请说明理由．
请考生在22，23，24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时用2B铅笔在答题卡把所选题目的题号涂黑．

Answer 1

分析：（I）先求出其导函数以及导数为0的根，通过比较两根的大小找到函数的单调区间，进而求出f（x）的极小值；
（II）对于存在性问题，可先假设存在，即假设存在常数a，使函数y=f（x）在区间[m，n]上存在零点，再利用零点存在定理得出不等式：lna≥

a

2

+1，下面利用 导数证明此不等式不成立，出现矛盾，则说明假设不成立，即不存在；否则存在．

解答：解：（Ⅰ）  f′(x)=x-(1+a)+

a

x

=

x2-(1+a)x+a

x

=

(x-1)(x-a)

x

令f'（x）=0，得到x₁=1，x₂=a．
（1）当a=1时，f（x）在定义域单调递增，没有极小值点．
（2）当a＞1时，x变化时．f′（x），f（x）的变化情况如表：

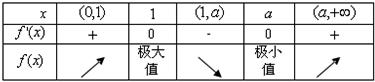
所以x=1是函数的极大值点，x=a是函数的极小值点；
（3）当0＜a＜1时，x变化时．f′（x），f（x）的变化情况如表：

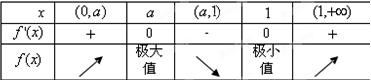
所以x=1是函数的极小值点，x=a是函数的极大值点；
综上所述．当0＜a＜1时，x=1是函数的极小值点；当a＞1时，x=a是函数的极小值点；
（II）若曲线y=f（x）在点A（m，f（m）），B（n，f（n））处的切线都与y轴垂直，则f′（m）=0，f′（n）=0，
由（I）的讨论知，m=1，n=a或m=a，n=1，f（1）=-

1

2

-a，f（a）=-

a2

2

-a+alna．
∴函数y=f（x）在区间[m，n]上存在零点，且单调，则有f（1）f（a）≤0，
即（-

1

2

-a）（-

a2

2

-a+alna）≤0，
∴（

a2

2

+a-alna）≤0，故lna≥

a

2

+1，
下面证明此不等式不成立．
令g（a）=lna-

a

2

-1，则g′（a）=

1

a

-

1

2

=

2-a

2a

，
于是当a∈（0，2），g′（a）＞0，a∈（2，+∞），g′（a）＜0，
所以，g（a）在（0，2）单调递增，在[2，+∞）单调递减，
所以函数g(a)=lna-

a

2

-1在a=2取得最大值g（2）=ln2-2＜0．
所以g(a)=lna-

a

2

-1≤g(2)＜0，所以lna＜

a

2

+1．
故不存在满足要求的常数a．-------（12分）

点评：本题第一问考查利用导函数来研究函数的极值．在利用导函数来研究函数的极值时，分三步①求导函数，②求导函数为0的根，③判断根左右两侧的符号，若左正右负，原函数取极大值；若左负右正，原函数取极小值．