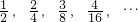练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    数列数学公式的前10项和S10=________．


    分析：数列的通项公式为an= 可看作由等差数列{n}和等比数列{}从第一项起对应相乘得到，可用错位相消法求解．
    解答：
    两边同乘以，得
    =
    两式相减得
    =
    =-
    =1--=
    ∴S10=
    故答案为：
    点评：本题考查数列求和的错位相消法．适用于形如{an•bn}前n项和，其中{an}是等差数列，{bn}是等比数列．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知数列{an}的前n项和Sn满足：S1=10，当n≥2时，2Sn=（n+4）an．
    （1）求a2，a3的值；  
    （2）求数列{an}的通项公式；
    （3）求
    1
    a2a3
    +
    1
    a3a4
    +…+
    1
    anan+1
    的值．

    查看答案和解析>>

    科目：高中数学 来源：2007年综合模拟数学卷五 题型：044

    记Sn为数列{an}的前n项和，给出两个数列：

    ①5，3，1，－1，－3，－5，－7，……

    ②―14，―10，―6，―2，2，6，10，14，18，……

    (1)对于数列①，计算S1，S2，S4，S5；对于数列②，计算S1，S3，S5，S7；

    (2)根据上述结果，对于存在正整数k，满足ak＋ak+1＝0的等差数列{an}，求证：Sn＝S2k－n．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知数列{an}的前n项和Sn满足：S1=10，当n≥2时，2Sn=（n+4）an．
    （1）求a2，a3的值；　
    （2）求数列{an}的通项公式；
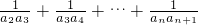    （3）求数学公式的值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知数列{an}的前n项和Sn满足：S1=10，当n≥2时，2Sn=（n+4）an．
    （1）求a2，a3的值；  
    （2）求数列{an}的通项公式；
    （3）求
    1
    a2a3
    +
    1
    a3a4
    +…+
    1
    anan+1
    的值．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年四川省资阳外国语实验学校高三适应性考试数学试卷（解析版） 题型：解答题

    已知数列{an}的前n项和Sn满足：S1=10，当n≥2时，2Sn=（n+4）an．
    （1）求a2，a3的值；  
    （2）求数列{an}的通项公式；
    （3）求的值．

    查看答案和解析>>

    同步练习册答案