Question

9．已知△ABC是半径为5的圆O的内接三角形，且tanA=$\frac{4}{3}$，若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$（x，y∈R），则x+y的最大值为$\frac{5}{8}$．

Answer 1

分析 延长AO与BC相交于点D，作OA₁∥DA₂∥AB，OB₁∥DB₂∥AC，设$\overrightarrow{AD}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$（m＞0，n＞0），推出$\frac{m}{x}=\frac{n}{y}$=$\frac{AD}{AO}$，结合B、D、C三点共线，得到x+y的表达式，利用三角代换，求解最值即可．

解答 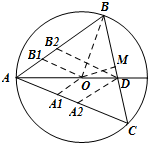解：延长AO与BC相交于点D，作OA₁∥DA₂∥AB，OB₁∥DB₂∥AC，
设$\overrightarrow{AD}$=m$\overrightarrow{AB}$+n$\overrightarrow{AC}$（m＞0，n＞0），易知x＞0，y＞0，
则$\frac{m}{x}=\frac{n}{y}$=$\frac{AD}{AO}$，
∴$\overrightarrow{AD}$=x•$\frac{AD}{AO}$•$\overrightarrow{AB}$+y•$\frac{AD}{AO}$•$\overrightarrow{AC}$，
又B、D、C三点共线，∴x•$\frac{AD}{AO}$+y•$\frac{AD}{AO}$=1，
∴x+y=$\frac{AO}{AD}$=$\frac{1}{1+\frac{OD}{AO}}$，
只需$\frac{OD}{AO}$最小，就能使x+y最大，
∴当OD最小即可，过点O作OM⊥BC于点M，从而OD≥OM，
又∠BOM=∠BAC=θ，由tanA=$\frac{4}{3}$得cosθ=$\frac{3}{5}$=$\frac{OM}{OB}$，
∴OM=3，
那么x+y≤$\frac{1}{1+\frac{3}{5}}$=$\frac{5}{8}$．
故答案为：$\frac{5}{8}$．

点评 本题考查向量在集合中的应用，三角代换以及共线向量的应用，是中档题．