
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2S |
| a+b+c |
| 3V |
| A+B+C+D |
| 3V |
| A+B+C+D |
科目:高中数学 来源: 题型:
 已知边长分别为a米和b米的矩形球场ABCD,在球场正中的上方悬挂一照明灯P,已知球场上各点照明亮度与灯光照射到这点光线和地面夹角的正弦成正比,与这点到灯的距离的平方成反比,若要使球场最边缘的点A获得最好的照明亮度,灯距地面的高度应为多少米?
已知边长分别为a米和b米的矩形球场ABCD,在球场正中的上方悬挂一照明灯P,已知球场上各点照明亮度与灯光照射到这点光线和地面夹角的正弦成正比,与这点到灯的距离的平方成反比,若要使球场最边缘的点A获得最好的照明亮度,灯距地面的高度应为多少米?查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| ||||
| 2 |
| ||||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2014届甘肃天水一中高二下学期期末考试文科数学试卷(解析版) 题型:填空题
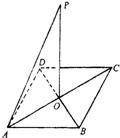
已知边长分别为a、b、c的三角形ABC面积为S,内切圆O半径为r,连接OA、OB、OC,则三角形OAB、OBC、OAC的面积分别为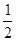 cr、
cr、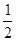 ar、
ar、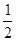 br,由S=
br,由S=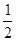 cr+
cr+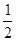 ar+
ar+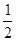 br得r=
br得r=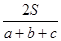 ,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
,类比得若四面体的体积为V,四个面的面积分别为A、B、C、D,则内切球的半径R=_____________.
查看答案和解析>>
科目:高中数学 来源:2011年高三数学复习(第5章 不等式):5.10 不等式的应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com