
分析 (Ⅰ)当a=1时,f(x)=x2-lnx,${f}^{'}(x)=2x-\frac{1}{x}$,由此利用导数的几何意义能求出函数f(x)在点(1,f(1))处的切线方程.
(Ⅱ)f(x)=ax2-lnx,a∈R的定义域为(0,+∞),${f}^{'}(x)=2ax-\frac{1}{x}$=$\frac{2a{x}^{2}-1}{x}$,根据a≤0,a>$\frac{1}{2{e}^{2}}$,0<a≤$\frac{1}{2{e}^{2}}$分类讨论,能求出存在a=$\frac{{e}^{2}}{2}$,使函数f(x)在区间(0,e]上的最小值为$\frac{3}{2}$.
解答 解:(Ⅰ)当a=1时,f(x)=x2-lnx,f(1)=1,
${f}^{'}(x)=2x-\frac{1}{x}$,f′(1)=1,
∴函数f(x)在点(1,f(1))处的切线方程为x-y=0.
(Ⅱ)∵f(x)=ax2-lnx,a∈R,∴此函数的定义域为(0,+∞),
${f}^{'}(x)=2ax-\frac{1}{x}$=$\frac{2a{x}^{2}-1}{x}$,
当a≤0时,f′(x)<0恒成立,∴f(x)在(0,e]上是减函数,
∴当x=e时,f(x)取得最小值f(e)=ae2-1=$\frac{3}{2}$,
解得a=$\frac{5}{2{e}^{2}}$>0与a≤0矛盾;
当a>0时,令f′(x)=0,得${x}_{1}=-\frac{1}{\sqrt{2}a}$,${x}_{2}=\frac{1}{\sqrt{2}a}$,
在(0,$\frac{1}{\sqrt{2}}$)上,f′(x)<0,在($\frac{1}{\sqrt{2}a}$,+∞)上,f′(x)>0,
∴当$\frac{1}{\sqrt{2}a}$<e,即a>$\frac{1}{2{e}^{2}}$时,函数f(x)在(0,$\frac{1}{\sqrt{2a}}$)上是减函数,在($\frac{1}{\sqrt{2a}}$,e)上是增函数,
∴当x=$\frac{1}{\sqrt{2a}}$时,f(x)取得最小值$\frac{1}{2}-ln\frac{1}{\sqrt{2a}}$,
令$\frac{1}{2}-ln\frac{1}{\sqrt{2a}}$=$\frac{3}{2}$,得a=$\frac{{e}^{2}}{2}$,符合题意.
当$\frac{1}{\sqrt{2a}}$≥e,即0<a≤$\frac{1}{2{e}^{2}}$时,函数f(x)在(0,e]是减函数,
∴当x=e时,f(x)取得最小值,即ae2-1=$\frac{3}{2}$,
解得a=$\frac{5}{2{e}^{2}}$与0<a≤$\frac{1}{2{e}^{2}}$矛盾.
综上,存在a=$\frac{{e}^{2}}{2}$,使函数f(x)在区间(0,e]上的最小值为$\frac{3}{2}$.
点评 本题考查切线方程的求法,考查满足条件的实数值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{32}$ | B. | $\frac{37}{64}$ | C. | $\frac{19}{32}$ | D. | $\frac{27}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
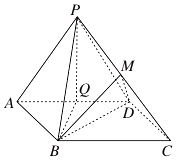 如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
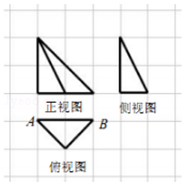 如图,网格上小正方形的边长为1,粗线画出的是一个三棱锥的三视图,该三棱锥的外接球的体积记为V1,俯视图绕底边AB所在直线旋转一周形成的几何体的体积记为V2,则V1:V2( )
如图,网格上小正方形的边长为1,粗线画出的是一个三棱锥的三视图,该三棱锥的外接球的体积记为V1,俯视图绕底边AB所在直线旋转一周形成的几何体的体积记为V2,则V1:V2( )| A. | 4$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | 4 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com