
 .
.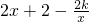 .
.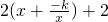 ≥
≥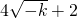 ,
,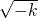 时,上述“≥”中取“=”.
时,上述“≥”中取“=”.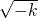 ∈(0,2],即当k∈[-4,0)时,
∈(0,2],即当k∈[-4,0)时,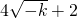 ;
;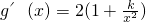 在(0,2]上为负恒成立,
在(0,2]上为负恒成立,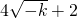 ;
; .切线的斜率k=f′(1)=2+2-2=2,由此能求出函数f(x) 在点P(1,4)处的切线方程.
.切线的斜率k=f′(1)=2+2-2=2,由此能求出函数f(x) 在点P(1,4)处的切线方程. 当且仅当a=b时取等号的方法求出最小值即可.
当且仅当a=b时取等号的方法求出最小值即可. 当且仅当a=b时取等号的灵活运用.本题有一定的探索性.综合性强,难度大,易出错.
当且仅当a=b时取等号的灵活运用.本题有一定的探索性.综合性强,难度大,易出错. 

科目:高中数学 来源: 题型:
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| 15 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:徐州模拟 题型:解答题
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省苏、锡、常、镇四市高三调研数学试卷(一)(解析版) 题型:解答题
 的最小值;
的最小值;查看答案和解析>>
科目:高中数学 来源:2011年江苏省苏州市高考数学一模试卷(解析版) 题型:解答题
 的最小值;
的最小值;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com