
| A. | $({-∞,\frac{2}{e}})$ | B. | ($\frac{2}{e}$,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | ($\frac{1}{e}$,+∞) |
分析 分类参数得a>$\frac{{e}^{2x}}{x+1}$,求出f(x)=$\frac{{e}^{2x}}{x+1}$在(-1,1]上的最小值即可得出a的范围.
解答 解:∵e2x-ax<a在(-1,1]上有解,∴a>$\frac{{e}^{2x}}{x+1}$在(-1,1]上有解,
令f(x)=$\frac{{e}^{2x}}{x+1}$,x∈(-1,1],则a>fmin(x).
则f′(x)=$\frac{{e}^{2x}(2x+1)}{(x+1)^{2}}$,
∴当x∈(-1,-$\frac{1}{2}$)时,f′(x)<0,当x∈(-$\frac{1}{2}$,1]时,f′(x)>0,
∴f(x)在(-1,-$\frac{1}{2}$]上单调递减,在(-$\frac{1}{2}$,1]上单调递增,
∴当x=-$\frac{1}{2}$时,f(x)取得最小值f(-$\frac{1}{2}$)=$\frac{2}{e}$.
∴a>$\frac{2}{e}$.
故选B.
点评 本题考查了函数的存在性问题与函数最值的计算,导数与函数单调性判断,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
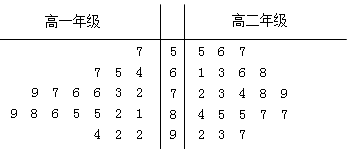
| A. | 高一学生满意度评分的平均值比高二学生满意度评分的平均值高 | |
| B. | 高一学生满意度评分比较集中,高二学生满意度评分比较分散 | |
| C. | 高一学生满意度评分的中位数为80 | |
| D. | 高二学生满意度评分的中位数为74 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 120 | C. | 2400 | D. | 14400 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com