
分析 (1)求出f(x)的导数,可得切线的斜率和切点,解方程可得a的值;
(2)求出f(x)=lnx+x,要证原不等式成立,即证xlnx+x-k(x-3)>0,可令g(x)=xlnx+x-k(x-3),求出导数,判断符号,可得单调性,即可得证;
(3)对于在(0,1)中的任意一个常数b,假设存在正数x0,使得e${\;}^{f({x}_{0}+1)-3{x}_{0}-2}$+$\frac{b}{2}$x02<1.运用转化思想可令H(x)=(x+1)•e-x+$\frac{b}{2}$x2-1,求出导数判断单调性,可得最小值,即可得到结论
解答 解:(1)函数f(x)=lnx+ax的导数为f′(x)=$\frac{1}{x}$+a,
在点(t,f(t))处切线方程为y=3x+1,
可得f′(t)=$\frac{1}{t}$+a,
∴函数的切线方程为y-(lnt+at)=($\frac{1}{t}$+a)(x-t),即y=($\frac{1}{t}$+a)x+lnt-1,
∴$\left\{\begin{array}{l}{\frac{1}{t}+a=3}\\{lnt-1=-1}\end{array}\right.$,
解得a=2;
(2)证明:由(1)可得f(x)=lnx+2x,
∵f(x)>k(1-$\frac{3}{x}$)+2x-1,
∴lnx>k(1-$\frac{3}{x}$)-1
即为xlnx+x-k(x-3)>0,
可令g(x)=xlnx+x-k(x-3),
g′(x)=2+lnx-k,
由x>1,可得lnx>0,2-k≥0,
即有g′(x)>0,g(x)在(1,+∞)递增,
可得g(x)>g(1)=1+2k≥0,
∴-$\frac{1}{2}$≤k≤2
故k的取值范围为[-$\frac{1}{2}$,2];
(3)对于在(0,1)中的任意一个常数b,
假设存在正数x0,使得:e${\;}^{f({x}_{0}+1)-3{x}_{0}-2}$+$\frac{b}{2}$x02<1.
由ef(x0+1)-3x0-2+$\frac{b}{2}$x02=eln(x0+1)-x0+$\frac{b}{2}$x02=(x0+1)•e-x0+$\frac{b}{2}$x02<1成立,
从而存在正数x0,使得上式成立,只需上式的最小值小于0即可.
令H(x)=(x+1)•e-x+$\frac{b}{2}$x2-1,H′(x)=e-x-(x+1)•e-x+bx=x(b-e-x),
令H′(x)>0,解得x>-lnb,令H′(x)<0,解得0<x<-lnb,
则x=-lnb为函数H(x)的极小值点,即为最小值点.
故H(x)的最小值为H(-lnb)=(-lnb+1)elnb+$\frac{b}{2}$ln2b-1=$\frac{b}{2}$ln2b-blnb+b-1,
再令G(x)=$\frac{x}{2}$ln2x-xlnx+x-1,(0<x<1),
G′(x)=$\frac{1}{2}$(ln2x+2lnx)-(1+lnx)+1=ln2x>0,
则G(x)在(0,1)递增,可得G(x)<G(1)=0,则H(-lnb)<0.
故存在正数x0=-lnb,使得e${\;}^{f({x}_{0}+1)-3{x}_{0}-2}$+$\frac{b}{2}$x02<1.
点评 本题考查导数的运用:求切线的斜率、单调区间和极值、最值,考查不等式的证明,注意运用分析法和构造函数法,求得导数判断单调性,考查存在性问题的解法,注意运用转化思想和构造函数,求出导数,运用单调性,属于难题.


 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | m(1+q)4元 | B. | m(1+q)5元 | C. | $\frac{m[(1+q)^{4}-(1+q)]}{q}$元 | D. | $\frac{m[(1+q)^{5}-(1+q)]}{q}$元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+(y+1)2=3 | B. | (x+2)2+(y-1)2=3 | C. | (x-2)2+(y+1)2=9 | D. | (x+2)2+(y-1)2=9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
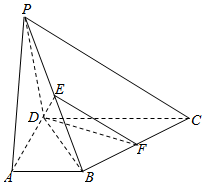 在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点.
在四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,DC=2AB=2AD,BC⊥PD,E,F分别是PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,\frac{2}{e}})$ | B. | ($\frac{2}{e}$,+∞) | C. | $({-∞,\frac{1}{e}})$ | D. | ($\frac{1}{e}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com