练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．在2013年至2016年期间，甲每年6月1日都到银行存入m元的一年定期储蓄，若年利率为q保持不变，且每年到期的存款本息自动转为新的一年定期，到2017年6月1日甲去银行不再存款，而是将所有存款的本息全部取回，则取回的金额是（　　）
    A．m（1+q）4元B．m（1+q）5元C．$\frac{m[（1+q）^{4}-（1+q）]}{q}$元D．$\frac{m[（1+q）^{5}-（1+q）]}{q}$元

    分析 2013年6月1日到银行存入m元的一年定期储蓄，到2017年6月1日本息和为：m（1+q）4，2014年6月1日到银行存入m元的一年定期储蓄，到2017年6月1日本息和为：m（1+q）3，2015年6月1日到银行存入m元的一年定期储蓄，到2017年6月1日本息和为：m（1+q）2，2016年6月1日到银行存入m元的一年定期储蓄，到2017年6月1日本息和为：m（1+q），由此利用等比数列前n项和公式能求出到2017年6月1日甲去银行将所有存款的本息全部取回，取回的金额．

    解答 解：2013年6月1日到银行存入m元的一年定期储蓄，到2017年6月1日本息和为：m（1+q）4，
    2014年6月1日到银行存入m元的一年定期储蓄，到2017年6月1日本息和为：m（1+q）3，
    2015年6月1日到银行存入m元的一年定期储蓄，到2017年6月1日本息和为：m（1+q）2，
    2016年6月1日到银行存入m元的一年定期储蓄，到2017年6月1日本息和为：m（1+q），
    ∴到2017年6月1日甲去银行将所有存款的本息全部取回，则取回的金额是：
    S=m（1+q）（1+q）+m（1+q）2+m（1+q）3+m（1+q）4=$\frac{m（1+q）[1-（1+q）^{4}]}{1-（1+q）}$=$\frac{m[（1+q）^{5}-（1+q）]}{q}$．
    故选：D．

    点评 本题考查等比数列的前四项和的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知f（x）=ax3-x2-x+b（a，b∈R，a≠0），g（x）=$\frac{{3\sqrt{e}}}{4}{e^x}$（e是自然对数的底数），f（x）的图象在x=-$\frac{1}{2}$处的切线方程为y=$\frac{3}{4}x+\frac{9}{8}$．
    （1）求a，b的值；
    （2）探究直线y=$\frac{3}{4}x+\frac{9}{8}$．是否可以与函数g（x）的图象相切？若可以，写出切点的坐标，否则，说明理由；
    （3）证明：当x∈（-∞，2]时，f（x）≤g（x）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设不等式$\left\{\begin{array}{l}{y＞1}\\{2x-y≥0}\end{array}\right.$，表示的平面区域为D．若曲线y=ax2+1上存在无数个点在D内，则实数a的取值范围是（　　）
    A．（0，2）B．（1，+∞）C．（0，1）D．（-∞，2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．2017年2月为确保食品安全，鞍山市质检部门检查1000袋方便面的质量，抽查总量的2%，在这个问题中，下列说法正确的是（　　）
    A．总体是指这箱1000袋方便面B．个体是一袋方便面
    C．样本是按2%抽取的20袋方便面D．样本容量为20

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．在△ABC中，a，b，c分别为角A，B，C的对边，$B=\frac{2π}{3}$，若a2+c2=4ac，则$\frac{{sin（{A+C}）}}{sinAsinC}$=$\frac{10\sqrt{3}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

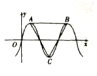    6．函数$f（x）=3\sqrt{3}sinωx（{ω＞0}）$的部分图象如图所示，点A，B是图象的最高点，点C是图象的最低点，且△ABC是正三角形，则f（1）+f（2）+f（3）的值为（　　）
    A．$\frac{9}{2}$B．$\frac{{9\sqrt{3}}}{2}$C．$9\sqrt{3}+1$D．$\frac{{9（{\sqrt{3}+1}）}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．设全集U=R，集合A={x|x2-3x≥0}，B={x∈N|x≤3}，则（∁UA）∩B等于（　　）
    A．∅B．{0，1}C．{1，2}D．{1，2，3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）上任意一点M与左右顶点A1、A2连线的斜率之积为$\frac{3}{4}$，则双曲线的离心率为（　　）
    A．$\frac{\sqrt{3}}{2}$B．$\frac{5}{4}$C．$\frac{\sqrt{7}}{2}$D．$\frac{5}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=lnx+ax在点（t，f（t））处的切线方程为y=3x+1
    （1）求a的值；
    （2）已知k≤2，当x＞1时，f（x）＞k（1-$\frac{3}{x}$）+2x-1恒成立，求实数k的取值范围；
    （3）对于在（0，1）中的任意一个常数b，是否存在正数x0，使得e${\;}^{f（{x}_{0}+1）-3{x}_{0}-2}$+$\frac{b}{2}$x02＜1？请说明理由．

    查看答案和解析>>

    同步练习册答案