
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
分析 由新定义可知,若数列{an}有H值,则数列不是单调数列,且存在k(k≥2,k∈N*),使得“ak>ak-1且ak>ak+1”成立.
①是等差数列,为单调数列;举例说明②存在H值;利用导数判断函数的单调性,说明③存在H值,④是单调数列.
解答 解:由新定义可知,若数列{an}有H值,则数列不是单调数列,且存在k(k≥2,k∈N*),使得“ak>ak-1且ak>ak+1”成立.
对于①an=1-2n,该数列为递减数列,不合题意;
对于②an=sinn,取k=2,则sin2>sin1,且sin2>sin3,数列存在H值;
对于③an=$\frac{n-2}{{e}^{n-3}}$,令f(x)=$\frac{x-2}{{e}^{x-3}}$,f′(x)=$\frac{3-x}{{e}^{x-3}}$,由f′(x)=0,得x=3.
当x<3时,f′(x)>0,函数为增函数,当x>3时,f′(x)<0,函数为减函数,∴x=3时函数取得极大值,也就是最大值,
则对于数列an=$\frac{n-2}{{e}^{n-3}}$,有a3>a2,且a3>a4,数列存在H值;
对于④an=lnn-n,令g(x)=lnx-x,g′(x)=$\frac{1}{x}-1=\frac{1-x}{x}$,当x≥1时,g′(x)≤0,数列为递减数列,不合题意.
∴存在H值的数列为②③.
故选:B.
点评 本题考查命题的真假判断与应用,考查数列的函数特性,训练了利用导数研究函数的单调性,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 总体是指这箱1000袋方便面 | B. | 个体是一袋方便面 | ||
| C. | 样本是按2%抽取的20袋方便面 | D. | 样本容量为20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{5}{4}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1,2} | B. | {-1,0} | C. | {-1,0,1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
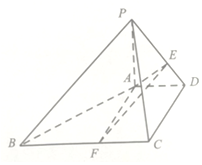 如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD
如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com