
| A. | 20 | B. | -20 | C. | -540 | D. | 540 |
分析 求定积分得a的值,再利用二项式展开式的通项公式求出展开式的常数项.
解答 解:$a=\int_0^2{xdx}$=$\frac{1}{2}$x2${|}_{0}^{2}$=$\frac{1}{2}$×22=2,
∴二项式${(x-\frac{a+1}{x})^6}$=${(x-\frac{3}{x})}^{6}$展开式中,
通项公式为Tr+1=${C}_{6}^{r}$•x6-r•${(-\frac{3}{x})}^{r}$=(-3)r•${C}_{6}^{r}$•x6-2r,
令6-2r=0,解得r=3;
∴展开式的常数项为:
T4=(-3)3•${C}_{6}^{3}$=-540.
故选:C.
点评 本题考查了定积分的计算问题,也考查了二项式展开式的通项公式应用问题,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
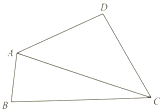 在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.
在四边形ABCD中,∠BAD=120°,∠BCD=60°,cosD=-$\frac{1}{7}$,AD=DC=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{6},\sqrt{7}}]$ | B. | $({0,\sqrt{7}}]$ | C. | $({\frac{{2\sqrt{42}}}{5},\sqrt{7}}]$ | D. | (6,7] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com