
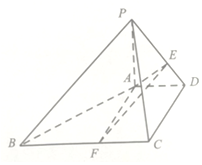
 如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD
如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD分析 (Ⅰ)连接BD,交AF于G,则△AGD∽△FGB,由已知可得$\frac{DE}{EP}=\frac{DG}{GB}$,则EG∥PB.再由线面平行的判定可得PB∥平面AEF;
(Ⅱ)证明AF⊥平面PAD,利用等积法结合三棱锥P-AEF的体积为$\frac{1}{3}$求λ的值.
解答 (Ⅰ)证明: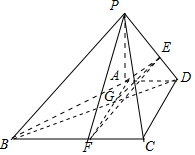 如图,
如图,
∵AD∥BC,AF∥CD,∴四边形AFCD为平行四边形,则CF=AD=1,
∵BC=3,∴BF=2,
连接BD,交AF于G,则△AGD∽△FGB,
∴$\frac{GD}{GB}=\frac{AD}{BF}=\frac{1}{2}$.
连接GE,∵PE=$\frac{2}{3}$PD,∴$\frac{DE}{EP}=\frac{1}{2}$,
∴$\frac{DE}{EP}=\frac{DG}{GB}$,则EG∥PB.
∵EG?平面AEF,PB?平面AEF,
∴PB∥平面AEF;
(Ⅱ)解:∵PA⊥平面ABCD,∴PA⊥AF,
由(Ⅰ)知AF∥CD,又CD⊥AD,
∴AF⊥AD,而PA∩AD=A,
∴AF⊥平面PAD.
∵PA=2AD=2,∴${S}_{△PAD}=\frac{1}{2}×2×1=1$,
∵PE=λPD,∴S△PAE=λ,
又AF=CD=2,
∴${V}_{P-AEF}={V}_{F-PAE}=\frac{1}{3}•λ•2=\frac{1}{3}$,得$λ=\frac{1}{2}$.
点评 本题考查线面平行的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 24 | C. | 30 | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①④ | D. | ③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理题 | 数学题 | 总计 | |
| 男同学 | 16 | 14 | 30 |
| 女同学 | 8 | 22 | 20 |
| 总计 | 24 | 36 | 60 |
| P(K2?k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| X | 3 | 4 | 5 | 6 |
| Y | 25 | 30 | 40 | 45 |
| A. | 59.5 | B. | 52.5 | C. | 56 | D. | 63.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com