
| 物理题 | 数学题 | 总计 | |
| 男同学 | 16 | 14 | 30 |
| 女同学 | 8 | 22 | 20 |
| 总计 | 24 | 36 | 60 |
| P(K2?k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)由表中数据求出K2≈4.444<6.635,从而得到在犯错误的概率不超过1%的前提下,不能判断高一学生对物理和数学的学习与性质有关.
(2)设甲、乙解答一道物理题的时间分别为x,y分钟,由甲每次解答一道物理题所用的时间为5-8分钟,乙每次解答一道物理题所用的时间为6-8分钟,利用几何概型能求出甲比乙先解答完的概率.
(3)由题意知在选择物理题的8名女生中任意抽取两人,抽取方法有${C}_{8}^{2}$=28种,X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(1)由表中数据得K2=$\frac{60×(16×22-14×8)^{2}}{30×30×24×36}$=$\frac{40}{9}$≈4.444<6.635,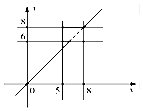
在犯错误的概率不超过1%的前提下,不能判断高一学生对物理和数学的学习与性质有关.
(2)设甲、乙解答一道物理题的时间分别为x,y分钟,
∵甲每次解答一道物理题所用的时间为5-8分钟,乙每次解答一道物理题所用的时间为6-8分钟,
∴$\left\{\begin{array}{l}{5≤x≤8}\\{6≤x≤8}\end{array}\right.$,设事件A表示“甲比乙先解答完”,则A表示“x<y”,
作出可行域,如右图:
∴甲比乙先解答完的概率P(A)=$1-\frac{\frac{1}{2}×2×2}{2×3}$=$\frac{2}{3}$.
(3)由题意知在选择物理题的8名女生中任意抽取两人,抽取方法有${C}_{8}^{2}$=28种,
其中甲、乙两人没有一个人被抽到有${C}_{6}^{2}=15$种,恰有一人被抽到有${C}_{2}^{1}{C}_{6}^{1}=12$种,两人都被抽到有${C}_{2}^{2}=1$种,
∴X的可能取值为0,1,2,
P(X=0)=$\frac{15}{28}$,P(X=1)=$\frac{12}{28}=\frac{3}{7}$,P(X=2)=$\frac{1}{28}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{15}{28}$ | $\frac{12}{28}$ | $\frac{1}{28}$ |
点评 本题考查独立检验的应用,考查概率的求法,考查离散型随机变量的分布列和数学期望,涉及几何概型、排列组合等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±$\sqrt{2}$ | C. | ±2 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [$\frac{1}{3}$,3] | C. | [$\frac{1}{6}$,2] | D. | [$\frac{1}{9}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
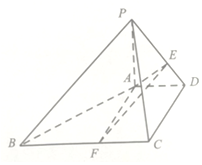 如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD
如图,在四棱锥P-ABCD中,∠ADC=90°,AD∥BC,$\frac{1}{3}$BC=$\frac{1}{2}$CD=AD=1,PA⊥平面ABCD,PA=2AD,E是线段PD上的点,设PE=λPD,F是BC上的点,且AF∥CD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{5}{36}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|2≤x≤3} | B. | {x|x≤2或x≥3} | C. | {x|2<x≤3} | D. | {x|x<2或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com