已知⊙Q:(x-1)2+y2=16,动⊙M过定点P(-1,0)且与⊙Q相切,则M点的轨迹方程是:
________.
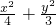
=1
分析:根据P(-1,0)在⊙Q内,可判断出⊙M与⊙Q内切,设⊙M的半径是为r,则可表示出|MQ|,进而根据⊙M过点P,求得|MP|=r,利用|MQ|=4|MP|,根据椭圆的定义可知其轨迹为椭圆,且焦点和长轴可知,进而求得椭圆方程中的b,则椭圆方程可得.
解答:P(-1,0)在⊙Q内,故⊙M与⊙Q内切,记:M(x,y),
⊙M的半径是为r,则:|MQ|=4-r,又⊙M过点P,
∴|MP|=r,
∴|MQ|=4-|MP|,即|MQ|+|MP|=4,
可见M点的轨迹是以P、Q为焦点(c=1)的椭圆,a=2.
∴b=
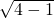
=

∴椭圆方程为:
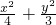
=1
故答案为:
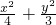
=1
点评:本题主要考查了椭圆的定义.考查了学生对数形结合思想的运用和对椭圆基础知识的掌握.

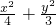 =1
=1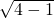 =
=
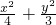 =1
=1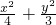 =1
=1
