
【题目】为预防![]() 病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于
病毒爆发,某生物技术公司研制出一种新流感疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于![]() %,则认为测试没有通过),公司选定
%,则认为测试没有通过),公司选定![]() 个流感样本分成三组,测试结果如下表:
个流感样本分成三组,测试结果如下表:
|
|
| |
疫苗有效 |
|
|
|
疫苗无效 |
|
|
|
已知在全体样本中随机抽取![]() 个,抽到
个,抽到![]() 组疫苗有效的概率是
组疫苗有效的概率是![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)现用分层抽样的方法在全体样本中抽取![]() 个测试结果,问应在
个测试结果,问应在![]() 组抽取多少个?
组抽取多少个?
(Ⅲ)已知![]() ,
,![]() ,求不能通过测试的概率.
,求不能通过测试的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由古典概型概率公式列方程求解即可;(2)先求出![]() 组样本个数,再根据分层抽样方法可得结果;(3)利用列举法可得基本事件空间包含的基本事件有11个,测试不能通过事件包含基本事件2个,利用古典概型概率公式可得结果.
组样本个数,再根据分层抽样方法可得结果;(3)利用列举法可得基本事件空间包含的基本事件有11个,测试不能通过事件包含基本事件2个,利用古典概型概率公式可得结果.
(1)![]() 在全体样本中随机抽取1个,抽到B组疫苗有效的概率约为其频率
在全体样本中随机抽取1个,抽到B组疫苗有效的概率约为其频率
即![]()
![]()
![]() ;
;
(2)C组样本个数为y+z=2000-(673+77+660+90)=500,
现用分层抽样的方法在全体样本中抽取360个测试结果,应在C组抽取个数为
![]() ;
;
(3)设测试不能通过事件为![]() 组疫苗有效与无效的可能的情况记为(
组疫苗有效与无效的可能的情况记为(![]() )由(2)知
)由(2)知![]() ,且
,且![]() ,基本事件空间包含的基本事件有:
,基本事件空间包含的基本事件有:
(465,35)、(466,34)、(467,33)、……(475,25)共11个
若测试不能通过,则77+90+z>200,即z>33
事件A包含的基本事件有:(465,35)、(466,34)共2个
![]()
![]() 故不能通过测试的概率为
故不能通过测试的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称AQI)是定量描述空气质量状况的质量指数.空气质量按照AQI大小分为六级:0~50为优;51~100为良;101~150为轻度污染;151~200为中度污染;201~300为重度污染;大于300为严重污染.一环保人士记录去年某地某月10天的AQI的茎叶图如图.利用该样本估计该地本月空气质量优良(![]() )的天数(按这个月总共30天计算)为________.
)的天数(按这个月总共30天计算)为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 的图象在
的图象在![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(2)是否存在负整数![]() ,使函数
,使函数![]() 的极大值为正值?若存在,求出所有负整数
的极大值为正值?若存在,求出所有负整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连续掷3枚硬币,观察落地后这3枚硬币出现正面还是反面.(与先后顺序有关)
(1)写出这个试验的样本空间及样本点的个数;
(2)写出事件“恰有两枚正面向上”的集合表示.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了参加某数学竞赛,某高级中学对高二年级理科、文科两个数学兴趣小组的同学进行了赛前模拟测试,成绩(单位:分)记录如下.
理科:79,81,81,79,94,92,85,89
文科:94,80,90,81,73,84,90,80
画出理科、文科两组同学成绩的茎叶图;

(2)计算理科、文科两组同学成绩的平均数和方差,并从统计学的角度分析,哪组同学在此次模拟测试中发挥比较好;
(3)若在成绩不低于90分的同学中随机抽出3人进行培训,求抽出的3人中既有理科组同学又有文科组同学的概率.
(参考公式:样本数据x1,x2,…,xn的方差:
s2=![]() [(x1-
[(x1-![]() )2+(x2-
)2+(x2-![]() )2+…+(xn-
)2+…+(xn-![]() )2],其中
)2],其中![]() 为样本平均数)
为样本平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国大学先修课程,是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备,某高中每年招收学生1000人,开设大学先修课程已有两年,共有300人参与学习先修课程,两年全校共有优等生200人,学习先修课程的优等生有50人,这两年学习先修课程的学生都参加了考试,并且都参加了某高校的自主招生考试(满分100分),结果如下表所示:

(1)填写列联表,并画出列联表的等高条形图,并通过图形判断学习先修课程与优等生是否有关系,根据列联表的独立性体验,能否在犯错误的概率不超过0.01的前提下认为学习先修课程与优等生有关系?

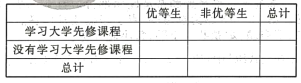
(2)已知今年有150名学生报名学习大学先修课程,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
①在今年参与大学先修课程的学生中任取一人,求他获得某高校自主招生通过的概率;
②某班有4名学生参加了大学先修课程的学习,设获得某高校自主招生通过的人数为![]() ,求
,求![]() 的分布列,并求今年全校参加大学先修课程的学生获得大学自主招生通过的人数.
的分布列,并求今年全校参加大学先修课程的学生获得大学自主招生通过的人数.
参考数据:

参考公式: ![]()
![]() ,期中
,期中![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校开展一次“五![]() 四”知识竞赛活动,共有三个问题,其中第1、2题满分都是15分,第3题满分是20分.每个问题或者得满分,或者得0分.活动结果显示,每个参赛选手至少答对一道题,有6名选手只答对其中一道题,有12名选手只答对其中两道题.答对第1题的人数与答对第2题的人数之和为26,答对第1的人数与答对第3题的人数之和为24,答对第2题的人数与答对第3题的人数之和为22.则参赛选手中三道题全答对的人数是____;所有参赛选手的平均分是____.
四”知识竞赛活动,共有三个问题,其中第1、2题满分都是15分,第3题满分是20分.每个问题或者得满分,或者得0分.活动结果显示,每个参赛选手至少答对一道题,有6名选手只答对其中一道题,有12名选手只答对其中两道题.答对第1题的人数与答对第2题的人数之和为26,答对第1的人数与答对第3题的人数之和为24,答对第2题的人数与答对第3题的人数之和为22.则参赛选手中三道题全答对的人数是____;所有参赛选手的平均分是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+1,g(x)=2alnx+1(a∈R)
(1)求函数h(x)=f(x)![]() g(x)的极值;
g(x)的极值;
(2)当a=e时,是否存在实数k,m,使得不等式g(x)≤ kx+m ≤f(x)恒成立?若存在,请求实数k,m的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com