
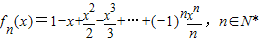 .
.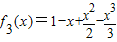 ,
,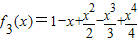 ,
,| x | (-∞,1) | (1,+∞) |
| f4′(x) | - | + |
| f4(x) | 减 | 增 |
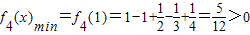 ,
,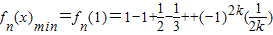 =
=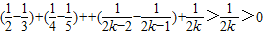
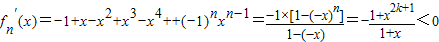 ;
;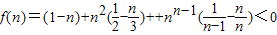 ,
,

 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:
 如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<
如图,将边长为3的正方形ABCD绕中心O顺时针旋转α (0<α<| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 2x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| v | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(07年福建卷理)(本小题满分14分)已知函数![]()
(Ⅰ)若![]() ,试确定函数
,试确定函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,且对于任意
,且对于任意![]() ,
,![]() 恒成立,试确定实数
恒成立,试确定实数![]() 的取值范围;
的取值范围;
(Ⅲ)设函数![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com