练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知抛物线y2=2px(p＞0),若有过动点M（a,0）且斜率为1的直线l与抛物线交于不同两点A、B，|AB|≤2p.(1)求a的取值范围；（2）若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值.

    思路解析：设出A、B两点的坐标，则得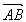Equation.3，（1）即求证|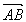Equation.3|≤2p;(2)若AB的垂直平分线交AB于Q，则可得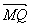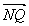Equation.3、Equation.3结合三角形面积公式易求.

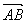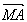    解：（1）设A（,y1）,B(,y2),则Equation.3=(,y2-y1),Equation.3=(-a,y1),

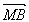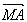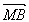    Equation.3=(-a,y2).  ∵Equation.3与Equation.3共线，∴（-a）y2-(-a)y1=0y1y2=-2pa.

    又直线l的斜率为1，∴y2-y1=y1+y2=2p.

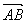    ∴|Equation.3|=|y2-y1|==.

    由0＜|AB|≤2p可得-＜a≤-.

    (2)设AB的垂直平分线交AB于点Q（x,y），则

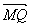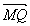    x==a+p,y==p,∴Equation.3=(p,p),|Equation.3|=p(定值).

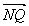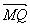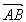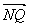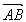    ∵|Equation.3|=|Equation.3|，∴S△NAB=|Equation.3|·|Equation.3|=p·|Equation.3|≤p2.

    ∴△NAB的最大面积为p2.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知抛物线y2=2px（p＞0）．过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，|AB|≤2p．
    （1）求a的取值范围；
    （2）若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线y2=2px（p＞0）的焦点为F，准线为l．
    （1）求抛物线上任意一点Q到定点N（2p，0）的最近距离；
    （2）过点F作一直线与抛物线相交于A，B两点，并在准线l上任取一点M，当M不在x轴上时，证明：
    kMA+kMBkMF
    是一个定值，并求出这个值．（其中kMA，kMB，kMF分别表示直线MA，MB，MF的斜率）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线y2=2px（p＞0）．过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，|AB|≤2p．求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•聊城一模）已知抛物线y2=2px（p＞0），过点M（2p，0）的直线与抛物线相交于A，B，
    OA
    •
    OB
    =
    0
    0
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知抛物线y2=2px（p＞0），M（2p，0），A、B是抛物线上的两点．求证：直线AB经过点M的充要条件是OA⊥OB，其中O是坐标原点．

    查看答案和解析>>

    同步练习册答案