
| A£® | 1 | B£® | 2 | C£® | $\sqrt{3}$ | D£® | $2\sqrt{3}$ |
·ÖÎö ÓÉÓÚ$|\overrightarrow{OA}|=1$£¬$|\overrightarrow{OB}|=4$£¬$\overrightarrow{OA}•\overrightarrow{OB}=2$£¬ÀûÓĂÊưÁ¿»ưÔËËăĐÔÖÊ¿ÉµĂ£º¡ÏAOB=$\frac{¦Đ}{3}$£®ÔÙÀûÓĂ¡÷ABCµÄĂæ»ưS=$\frac{1}{2}|\overrightarrow{OA}||\overrightarrow{OB}|sin\frac{¦Đ}{3}$¼´¿ÉµĂ³ö£®
½â´đ 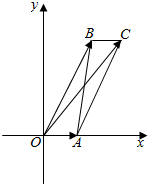 ½â£º¡ß$|\overrightarrow{OA}|=1$£¬$|\overrightarrow{OB}|=4$£¬$\overrightarrow{OA}•\overrightarrow{OB}=2$£¬
½â£º¡ß$|\overrightarrow{OA}|=1$£¬$|\overrightarrow{OB}|=4$£¬$\overrightarrow{OA}•\overrightarrow{OB}=2$£¬
¡à1¡Á4¡Ácos¡ÏAOB=2£¬
¡àcos¡ÏAOB=$\frac{1}{2}$£¬
¡à¡ÏAOB=$\frac{¦Đ}{3}$£®
¡à¡÷ABCµÄĂæ»ưS=$\frac{1}{2}|\overrightarrow{OA}||\overrightarrow{OB}|sin\frac{¦Đ}{3}$
=$\frac{1}{2}¡Á1¡Á4¡Á\frac{\sqrt{3}}{2}$
=$\sqrt{3}$£®
¹ÊÑ¡£ºC£®
µăÆÀ ±¾̀⿼²éÁËÈư½ÇĐÎĂæ»ư¼ÆËă¹«Ê½¡¢ÊưÁ¿»ưÔËËăĐÔÖÊ£¬¿¼²éÁËÍÆÀíÄÜÁ¦Óë¼ÆËăÄÜÁ¦£¬ÊôÓÚÖеµ̀⣮


 ÆÚÄ©¼¯½áºÅϵÁĐ´đ°¸
ÆÚÄ©¼¯½áºÅϵÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | µÚ̉»ÏóÏ̃ | B£® | µÚ¶₫ÏóÏ̃ | C£® | µÚÈưÏóÏ̃ | D£® | µÚËÄÏóÏ̃ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
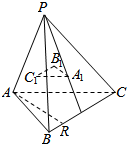 Èçͼ£¬PÊÇ¡÷ABCËùÔÚƽĂæÍâµÄ̉»µă£¬A1£¬B1£¬C1̉À´ÎÊÇ¡÷PBC£¬¡÷PAC£¬¡÷PABµÄÖØĐÄ£¬ARÊÇƽĂæABCÄÚµÄÈÎ̉ẩ»̀ơÖ±Ïߣ¬ÇóÖ¤£ºAR¡ÎƽĂæA1B1C1£®
Èçͼ£¬PÊÇ¡÷ABCËùÔÚƽĂæÍâµÄ̉»µă£¬A1£¬B1£¬C1̉À´ÎÊÇ¡÷PBC£¬¡÷PAC£¬¡÷PABµÄÖØĐÄ£¬ARÊÇƽĂæABCÄÚµÄÈÎ̉ẩ»̀ơÖ±Ïߣ¬ÇóÖ¤£ºAR¡ÎƽĂæA1B1C1£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | $\frac{\sqrt{¦Đ}}{3}$ | B£® | $\frac{\sqrt{¦Đ}}{2}$ | C£® | $\frac{\sqrt{3¦Đ}}{3}$ | D£® | $\frac{\sqrt{3¦Đ}}{2}$ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | ÓĐÇ̉Ö»ÓĐ̉»¸ö | B£® | ÓĐÇ̉Ö»ÓĐ3¸ö | C£® | ÓĐÎ̃Êư¸ö | D£® | ²»´æÔÚ |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£ºÑ¡Ôñ̀â
| A£® | 1 | B£® | 2 | C£® | 3 | D£® | 4 |
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com