
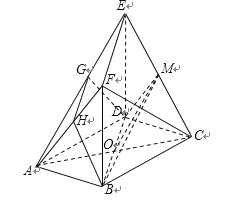
【题目】如图,在多面体![]() 中,底面
中,底面![]() 为正方形,四边形
为正方形,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若过直线![]() 的一个平面与线段
的一个平面与线段![]() 和
和![]() 分别相交于点
分别相交于点![]() 和
和![]() (点
(点![]() 与点
与点![]() 均不重合),求证:
均不重合),求证: ![]() ;
;
(3)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)要证面面垂直,先找线面垂直,证![]() 平面
平面![]() ,最终得到面面垂直;(2)根据线面平行的性质定理得到
,最终得到面面垂直;(2)根据线面平行的性质定理得到![]() 平面
平面![]() ,再由线面平行的判定定理得到结论;(3)取CE的中点M,证两个平面的两条相交直线互相平行,得到面面平行,进而得到比值。
,再由线面平行的判定定理得到结论;(3)取CE的中点M,证两个平面的两条相交直线互相平行,得到面面平行,进而得到比值。
解析:
(Ⅰ)因为四边形![]() 是正方形,
是正方形,
所以![]() .
.
又因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
且![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(Ⅱ)由题意, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅲ)线段![]() 上存在一点
上存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,此时
,此时![]() .
.
以下给出证明过程.
设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
, ![]() ,
,
因为![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
设![]() ,连接
,连接![]() ,
,
在![]() 中,因为
中,因为![]() ,
, ![]() ,
,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .又因为
.又因为![]() ,
, ![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知某海滨浴场海浪的高度y(米)是时间t(0≤t≤24,单位:时)的函数,记作:![]() .下表是某日各时的浪高数据.
.下表是某日各时的浪高数据.
t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求函数y=f(t)的函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8:00时至晚上20:00时之间,有多少时间可供冲浪者进行运动?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数 ![]() ,若曲线
,若曲线 ![]() 上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
上存在(x0 , y0),使得f(f(y0))=y0成立,则实数m的取值范围为( )
A.[0,e2﹣e+1]
B.[0,e2+e﹣1]
C.[0,e2+e+1]
D.[0,e2﹣e﹣1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆(x-3) 2+(y+4) 2=1关于直线x+y=0对称的圆的方程是( )
A. (x+3)2+(y-4)2=1
B. (x-4)2+(y+3)2=1
C. (x+4)2+(y-3)2=1
D. (x-3)2+(y-4)2=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]()
(1)若![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若曲线![]() 表示圆时,已知圆
表示圆时,已知圆![]() 与圆
与圆![]() 交于
交于![]() 两点,若弦
两点,若弦![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 为圆
为圆![]() 的直径,且圆
的直径,且圆![]() 过原点,求实数
过原点,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com