
【题目】已知数列{an}的前n项和为Sn , 满足 ![]() ,且a1=3.
,且a1=3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证: ![]() .
.
【答案】解:(Ⅰ)数列{an}的前n项和为Sn , 且 ![]() , ∴Sn﹣Sn﹣1=2an﹣1+1,(n≥2,n∈N*),
, ∴Sn﹣Sn﹣1=2an﹣1+1,(n≥2,n∈N*),
即an=2an﹣1+1(n≥2,n∈N*),
∴an+1=2(an﹣1+1),
∴数列{an+1}是等比数列;
又a1+1=3+1=4,
∴ ![]() ,
,
∴ ![]() ;
;
(Ⅱ)由(Ⅰ)知, ![]() ,
,
∴{ ![]() }是首项为
}是首项为 ![]() ,公比为
,公比为 ![]() 的等比数列,
的等比数列,
因此 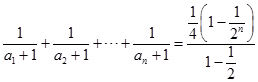
= ![]()
![]()
【解析】(Ⅰ)由数列{an}的前n项和与通项公式的定义,得出an=2an﹣1+1(n≥2,n∈N*),从而得出数列{an+1}是等比数列,由此求出{an}的通项公式; (Ⅱ)由(Ⅰ)写出数列{an+1}的通项公式,从而得出{ ![]() }是等比数列,求出其前n项和,即可证明不等式成立.
}是等比数列,求出其前n项和,即可证明不等式成立.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】把单位正方体的六个面分别染上6种颜色,并画上个数不同的金鸡,各面的颜色与鸡的个数对应如表:
面上所染颜色 | 红 | 黄 | 蓝 | 青 | 紫 | 绿 |
该面上的金鸡个数 | 1 | 2 | 3 | 4 | 5 | 6 |
取同样的4个上述的单位正方体拼成一个如图所示的水平放置的长方体.则这个长方体的下底面总计画有______个金鸡

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,抛物线y2=2px(p>0)的准线l与x轴交于点M,过点M的直线与抛物线交于A,B两点,设A(x1 , y1)到准线l的距离d=2λp(λ>0) 
(1)若y1=d=3,求抛物线的标准方程;
(2)若 ![]() +λ
+λ ![]() =
= ![]() ,求证:直线AB的斜率的平方为定值.
,求证:直线AB的斜率的平方为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上、下顶点、右顶点、右焦点分别为B2、B1、A、F,延长B1F与AB2交于点P,若∠B1PA为钝角,则此椭圆的离心率e的取值范围为_____.
的上、下顶点、右顶点、右焦点分别为B2、B1、A、F,延长B1F与AB2交于点P,若∠B1PA为钝角,则此椭圆的离心率e的取值范围为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人各有![]() 个材质、大小、形状完全相同的小球,甲的小球上面标有
个材质、大小、形状完全相同的小球,甲的小球上面标有![]() 五个数字,乙的小球上面标有
五个数字,乙的小球上面标有![]() 五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出
五个数字.把各自的小球放入两个不透明的口袋中,两人同时从各自的口袋中随机摸出![]() 个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
个小球.规定:若甲摸出的小球上的数字是乙摸出的小球上的数字的整数倍,则甲获胜,否则乙获胜.
(1)写出基本事件空间![]() ;
;
(2)你认为“规定”对甲、乙二人公平吗?说出你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点![]() 在正视图上的对应点为
在正视图上的对应点为![]() ,圆柱表面上的点
,圆柱表面上的点![]() 在左视图上的对应点为
在左视图上的对应点为![]() ,则在此圆柱侧面上,从
,则在此圆柱侧面上,从![]() 到
到![]() 的路径中,最短路径的长度为( )
的路径中,最短路径的长度为( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体![]() 中,底面
中,底面![]() 为正方形,四边形
为正方形,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若过直线![]() 的一个平面与线段
的一个平面与线段![]() 和
和![]() 分别相交于点
分别相交于点![]() 和
和![]() (点
(点![]() 与点
与点![]() 均不重合),求证:
均不重合),求证: ![]() ;
;
(3)判断线段![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率.
斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com