

(1)求证:CD⊥平面ABB1A1;
(2)求二面角A-A1B-C的平面角的正切值;
(3)求三棱锥B1—A1BC的体积;
(4)求BC1与平面A1BC所成角的正弦值.
(1)证明:∵ABC—A1B1C1是直三棱柱,?
∴面ABC⊥面AA1B1B,交线为AB.?
又∵△ABC是等腰三角形,∠ACB=90°,?∴CA=CB.?
又D是AB的中点,∴CD⊥AB.?
∴CD⊥平面AA1B1B.?
(2)解析:∵△ABC是等腰直角三角形,∴AB=![]() AC=
AC=![]() .?
.?
作DE⊥A1B于E,连结CE.?
由(1)知,CD⊥面AA1B1B,∴CE在面AA1B1B内的射影是DE.?
由三垂线定理知CE⊥A1B,?∴∠CED?是二面角C-A1B-A的平面角.?
又∵D是AB中点,?
∴DE=![]() DB=
DB=![]() .?
.?
又CD=![]() AB=
AB=![]() ,?
,?
在Rt△CDE中,tan∠CED=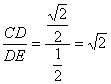 ,故二面角A-A1B-C的平面角的正切值为
,故二面角A-A1B-C的平面角的正切值为![]() .?
.?
(3)解析:由等积代换法得VB1—A1BC=VC—A1B1B?,∵AA1B1B是矩形,∴△AA1B的面积等于△A1B1B的面积.?
∴VC—A1B1B?=VC—AA1B?=![]() ·S△AA1B?·CD=
·S△AA1B?·CD=![]() .?
.?
∴VB1—A1BC?=![]() .?
.?
(4)解析:设C1B与面A1BC所成的角为θ,点C1到平面A1BC的距离为d.?
∴d=C1B·sinθ.又由直三棱柱性质得C1B=![]() .?
.?
C1到面A1BC的距离是以C1为顶点,△A1BC为底面的三棱锥C1—A1BC的高,∴VC1—A1BC=VB—A1C1C .?
∴△A1C1C的面积是矩形AA1C1C的面积的一半.?
∴S△A1C1C?=![]() .?
.?
∵BC⊥AC,CC1⊥BC,?
∴BC⊥面AA1C1C.?
∴VB—A1C1C?=![]() ×S△A1C1C ×BC=
×S△A1C1C ×BC=![]() .?
.?
又在△A1BC中,A1B=![]() =2,A1C=
=2,A1C=![]() ,BC=1,BC⊥A1C.?
,BC=1,BC⊥A1C.?
∴S△A1BC?=![]() ·A1C·BC?
·A1C·BC?
=![]() .?
.?
∴VC1—A1BC?=![]() .?
.?
∴![]() .?
.?
∴d=![]() .?
.?
又d=C1Bsinθ,即sinθ=![]() ,?
,?
∴sinθ=![]() ,?
,?
即BC1与平面A1BC所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
 如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点.
如图所示,直三棱柱ABC-A1B1C1的各条棱长均为a,D是侧棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记
如图所示,直三棱柱ABC-A1B1C1中,AB⊥AC,D,E分别为AA1,B1C的中点,若记| AB |
| a |
| AC |
| b |
| AA |
| c |
| DE |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 2 |
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| c |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.
如图所示,直三棱柱ABC-A'B'C'中,∠BCA=90°,CA=CB=1,AA'=2,M,N分别是A'B'、A'A的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求证:AB1∥平面BC1D;
(2)求异面直线AB1与BC1所成的角;
(3)求点A到平面BC1D的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com